運動学分析
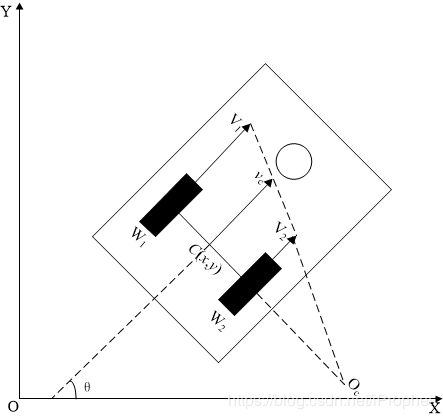
以上のイラストに示された、車軸中心Cの瞬間速度はv、回転角速度ω、回転半径rは、以下の数式で表される。
$$\begin{bmatrix}v\\ω\\r\end{bmatrix}=\begin{bmatrix}\frac{v_1 + v_2}{2}\\\frac{v_1 – v_2}{d}\\\frac{v}{ω}\end{bmatrix}=\begin{bmatrix}\frac{v_1 + v_2}{2}\\\frac{v_1 – v_2}{d}\\\frac{d}{2} \frac{v_1 + v_2}{v_1 – v_2}\end{bmatrix}$$
但し、d: 車輪間距離、v1: 左輪速度、v2: 右輪速度、ω: 角速度、r: 回転半径
運動状態分析
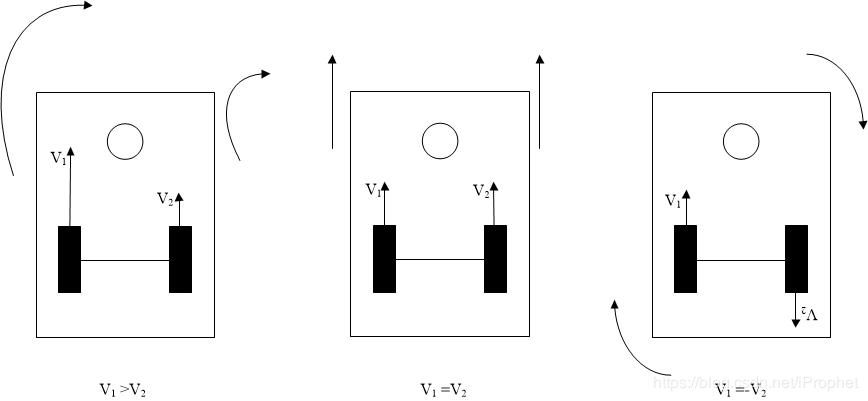
if v1 > v2 → ロボットが右方向へ回転する
if v1 = v2 → ロボットが直進または後退する
if v1 = -v2 → ロボットが車軸中心Cまわりに回転する、回転半径0m
運動学モデル
ロボット座標系からワールド座標系へ回転変換する際、2次元回転行列を用いる。
$$\begin{bmatrix}x_{t+1}\\x_{t+1}\\θ_{t+1}\end{bmatrix}=\begin{bmatrix}x_{t}\\x_{t}\\θ_{t}\end{bmatrix}+ \begin{bmatrix}cosθ&-sinθ&0\\sinθ&cosθ&0\\0&0&1\end{bmatrix}\begin{bmatrix}Δx_r\\Δy_r\\Δθ_r\end{bmatrix}$$
$$\begin{bmatrix}Δx_r\\Δy_r\\Δθ_r\end{bmatrix}=\begin{bmatrix}cosΔθ_r&0\\sinΔθ_r&0\\0&1\end{bmatrix}\begin{bmatrix}v_rΔt\\ω_rΔt\end{bmatrix}$$
また、他の計算方法があり、いずも近似式で、走行距離とともに誤差が累積していく。
ROSでは、上記情報のもとで、odomトピックを他のノードへブロードキャストし続ける。
