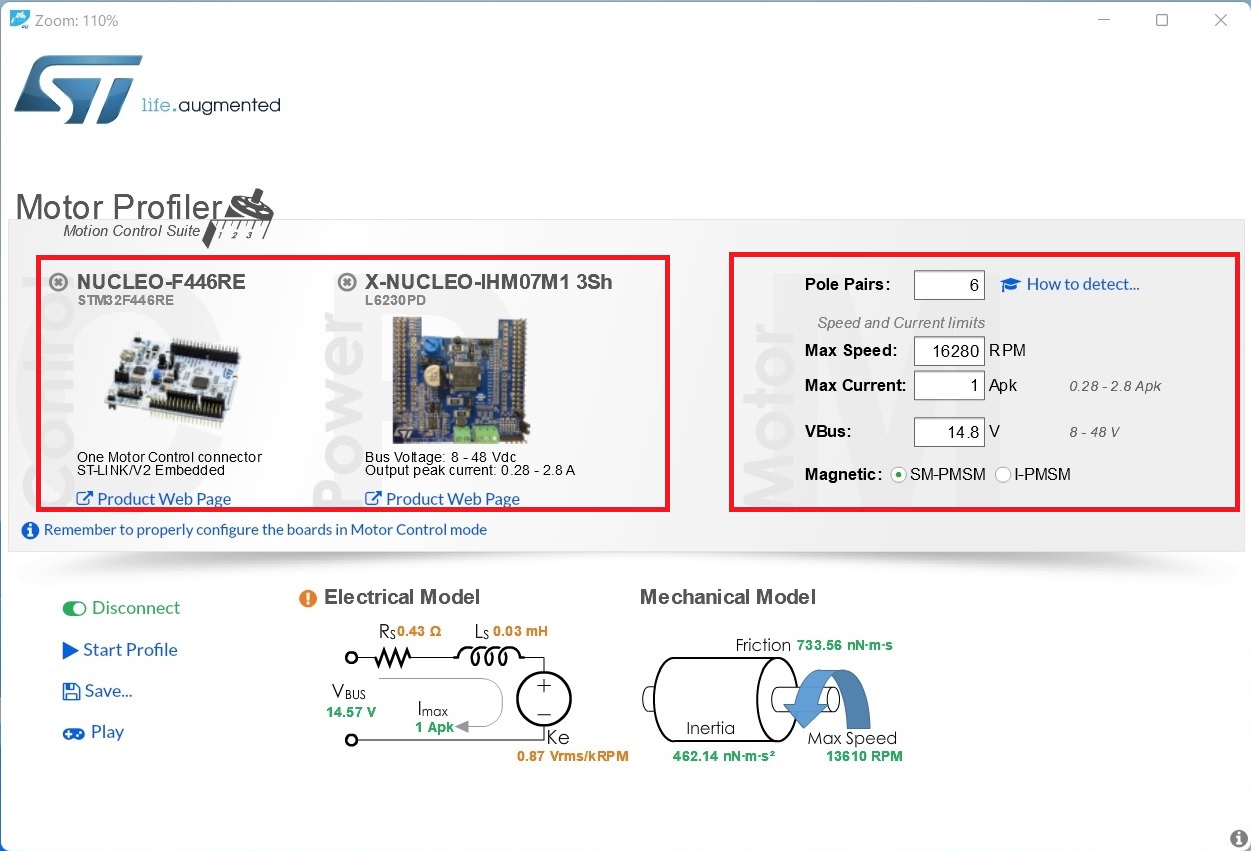
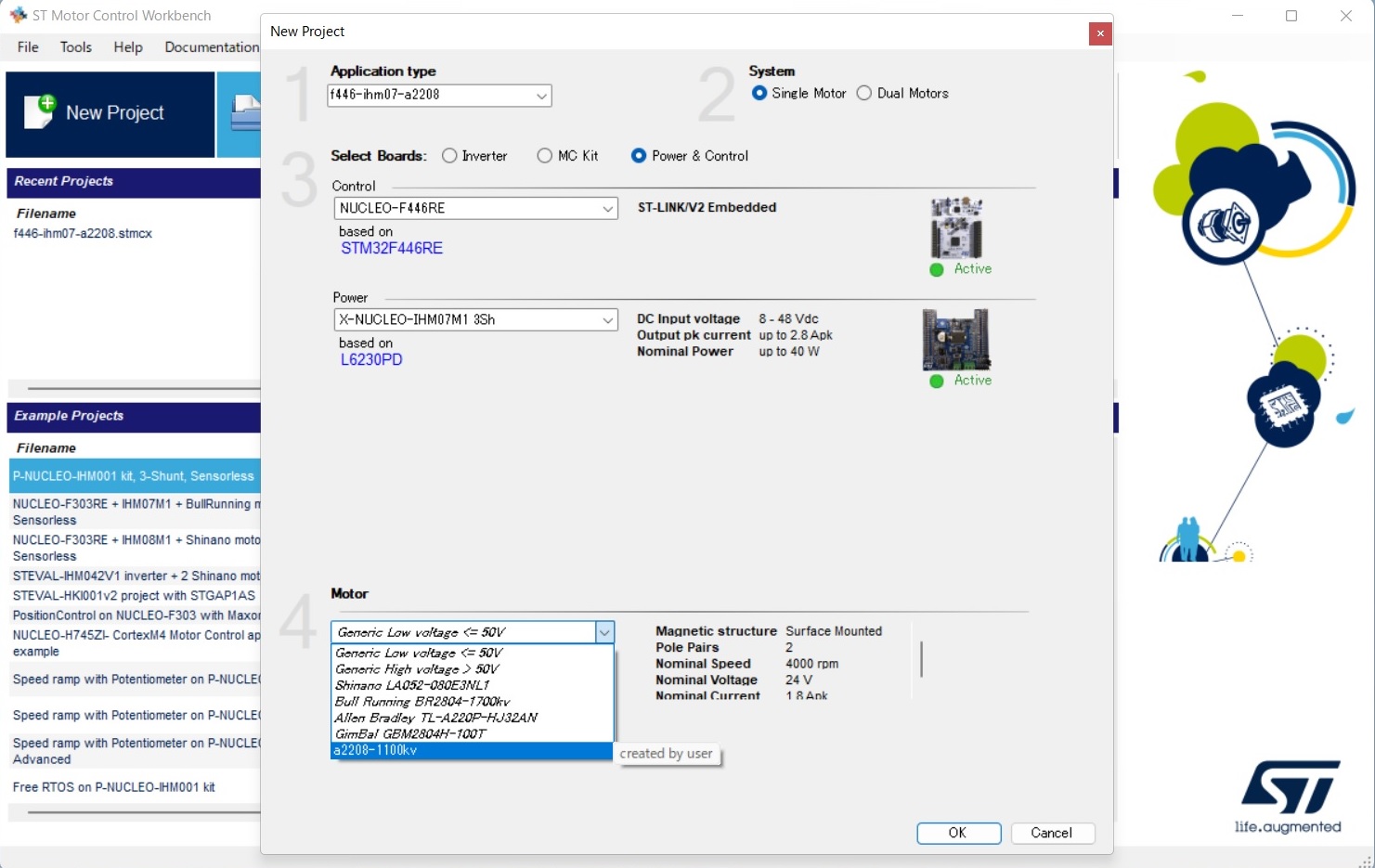
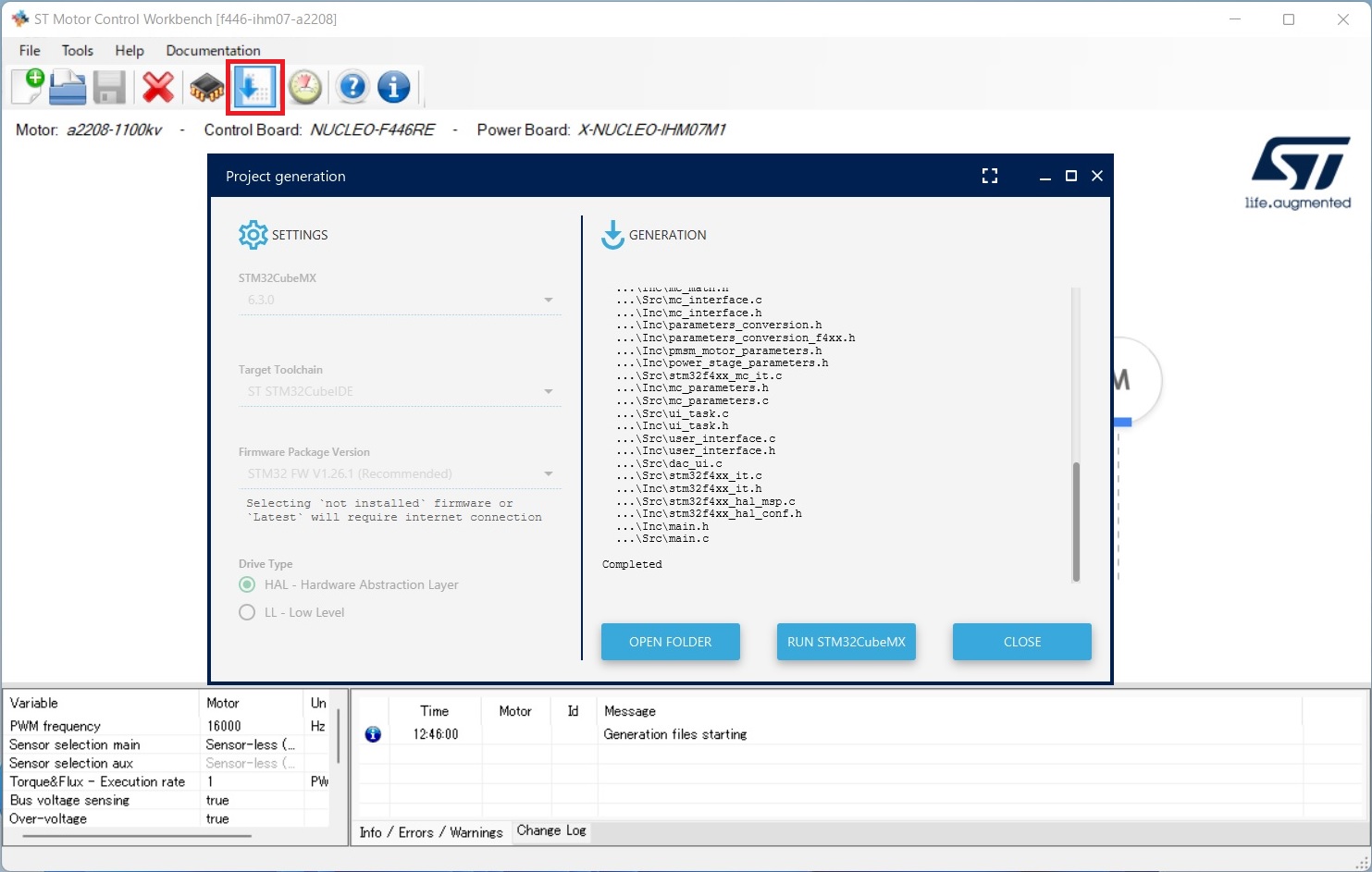
はじめに DCモータに対する、PID制御とは、制御量(本文では出力減速機シャフトの回転速度、角速度といい)と、目標値(本文ではターゲット回転速度、目標角速度といい)の差分(本文ではエラーといい)を無くすための操作量(PWMパルス出力)に関わる、P(比例)制御、I(積分)制御、D(微分)制御をかけるとのこと。ロータリエンコーダは回転速度を安易に計算可能な要素(A相/B相パルス)を提供する、常用デバイスとして利用される。本実験の趣旨としては、回転速度の計算ベースとなる、エンコーダのA/B相パルスは正しく計測されたかどうか、またPID制御の精度、確度を評価するに当たって、他のデバイス、本実験ではhayate_imu(ICM-20948内蔵)を活用して評価すること。
実験環境 ●12V入力DCブラシモータ
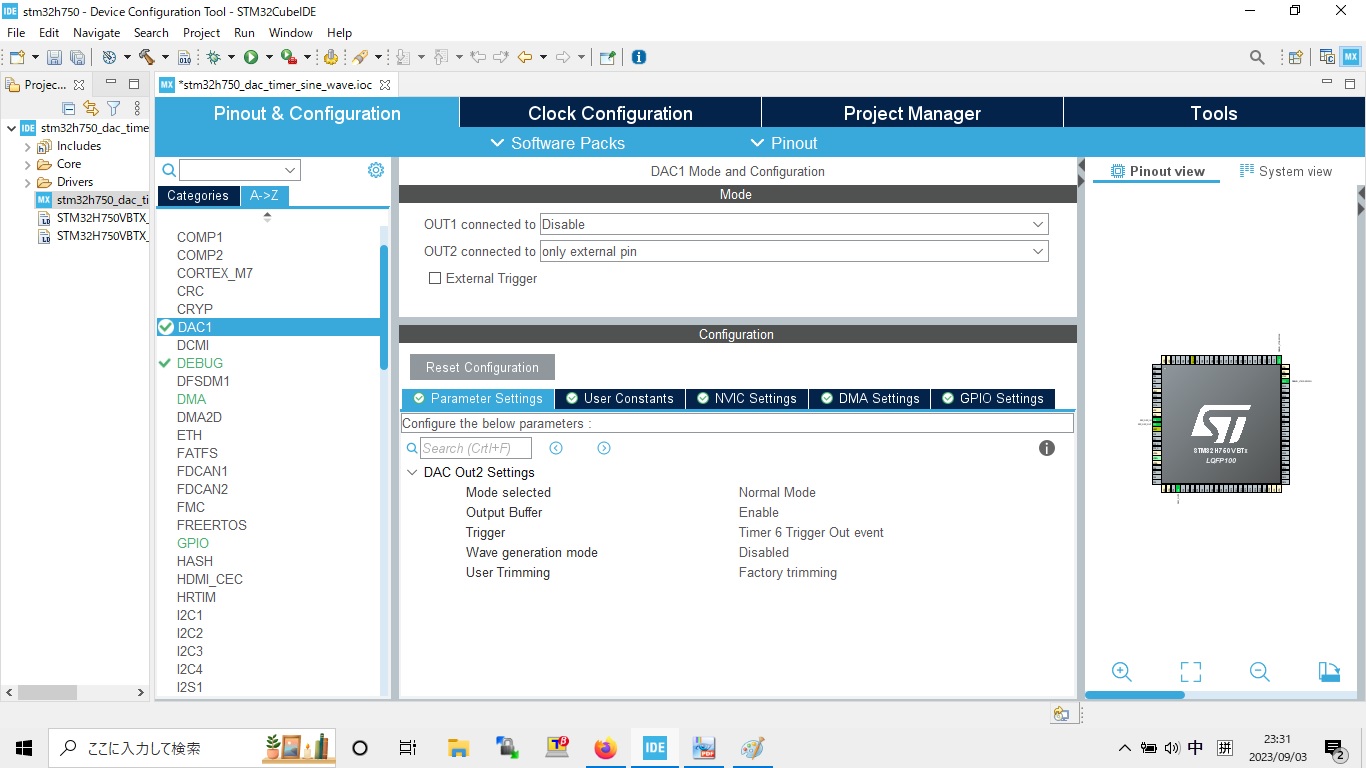
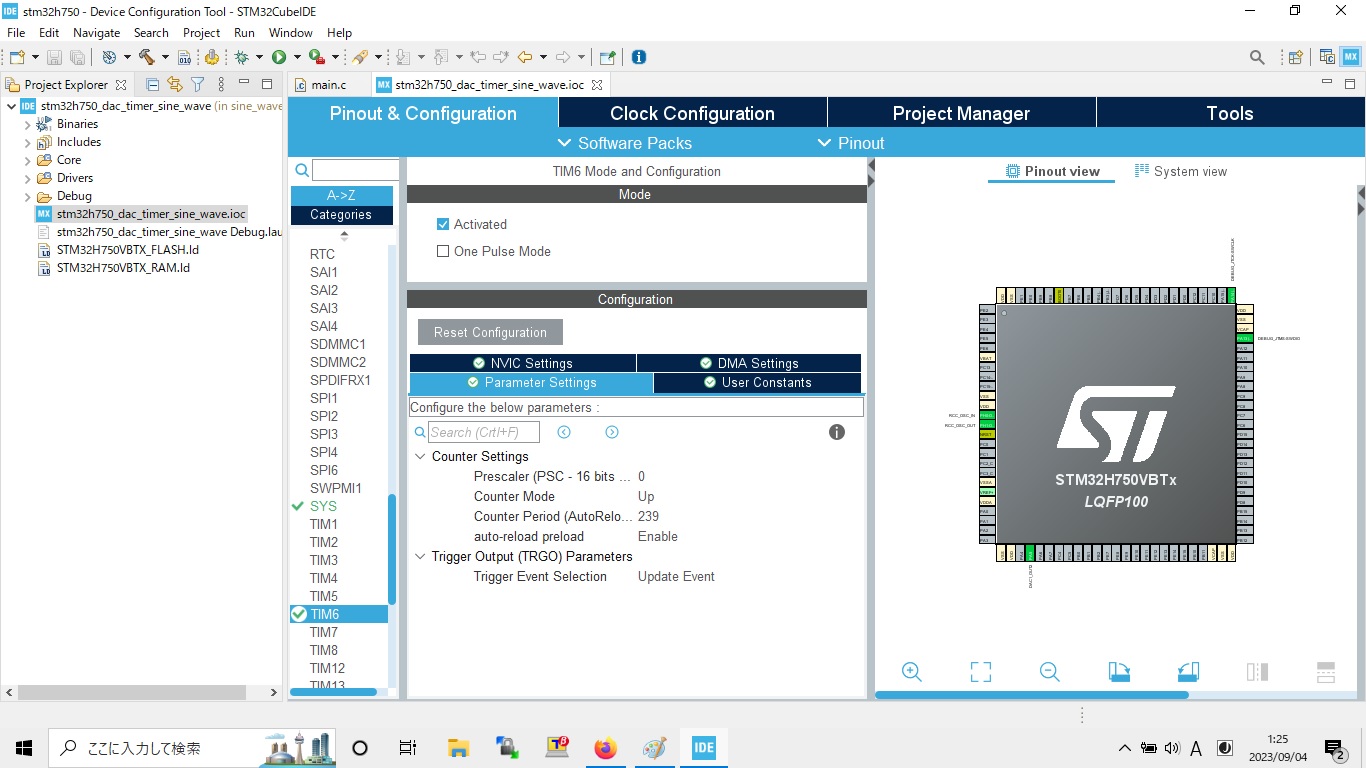
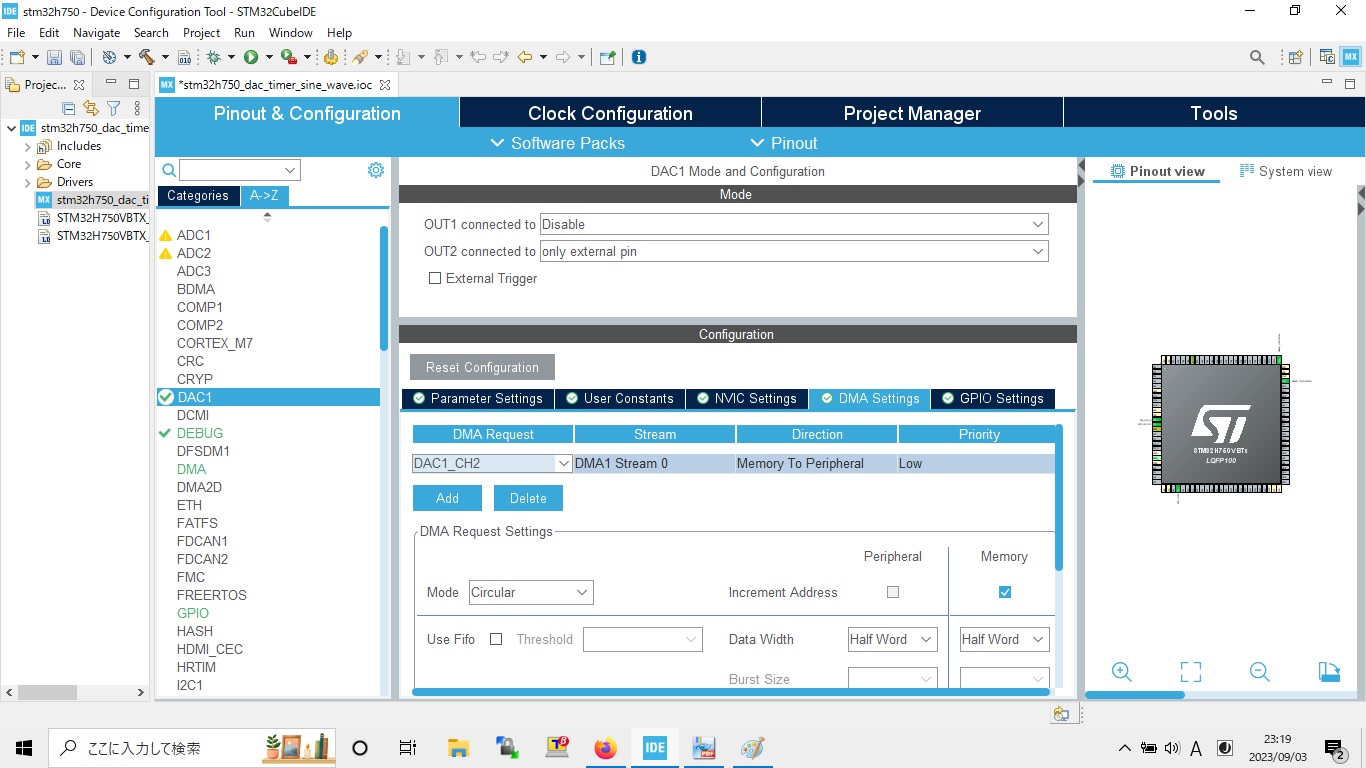
hayate_imu用いてDCモータPID制御評価環境 開発要素 ROSパッケージ 以下ROSパッケージ、ROSカスタムメッセージまたはライブラリをインストールして、catkin_makeしておく。
rosserial
hayate_motor_ros
hayate_imu_ros
ros_lib by rosserail_arduino with Arduino IDE
Adafruit-Motor-Shield-library-leonardo
arduino_node(ino) on Leonardo with Arduino IDE
ROSノード
/arduino_node
/hayate_imu_ros
/hayate_motor_node
/rosout
/rqt_plot
ROSトピック
/arduino_msg
/diagnostics
/hayate_angular_velocity_z
/imu_cali
/imu_data
/imu_demo
/pid_params
/rosout
/rosout_agg
ROSカスタムメッセージ
hayate_imu_ros/ImuCali
hayate_imu_ros/ImuData
hayate_motor_ros/ArduinoMsgs
hayate_motor_ros/PidMsgs
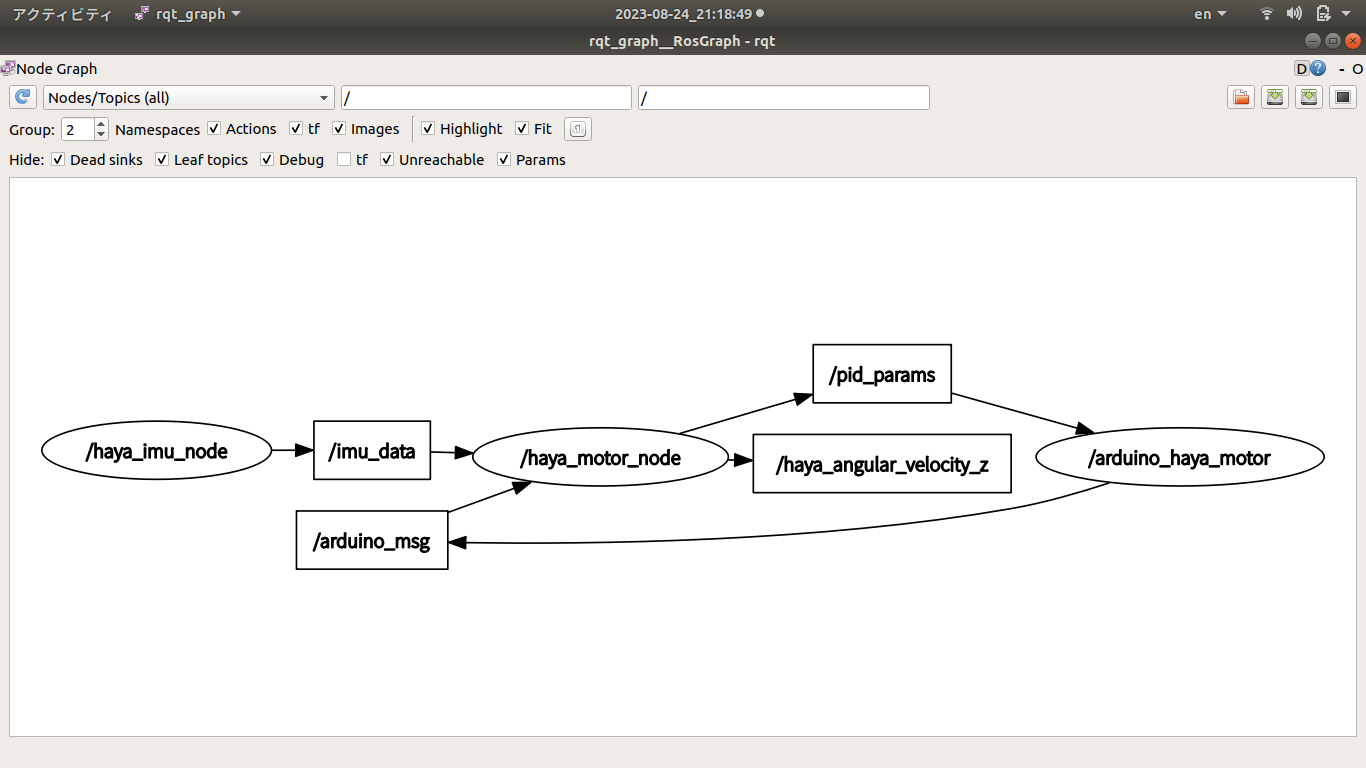
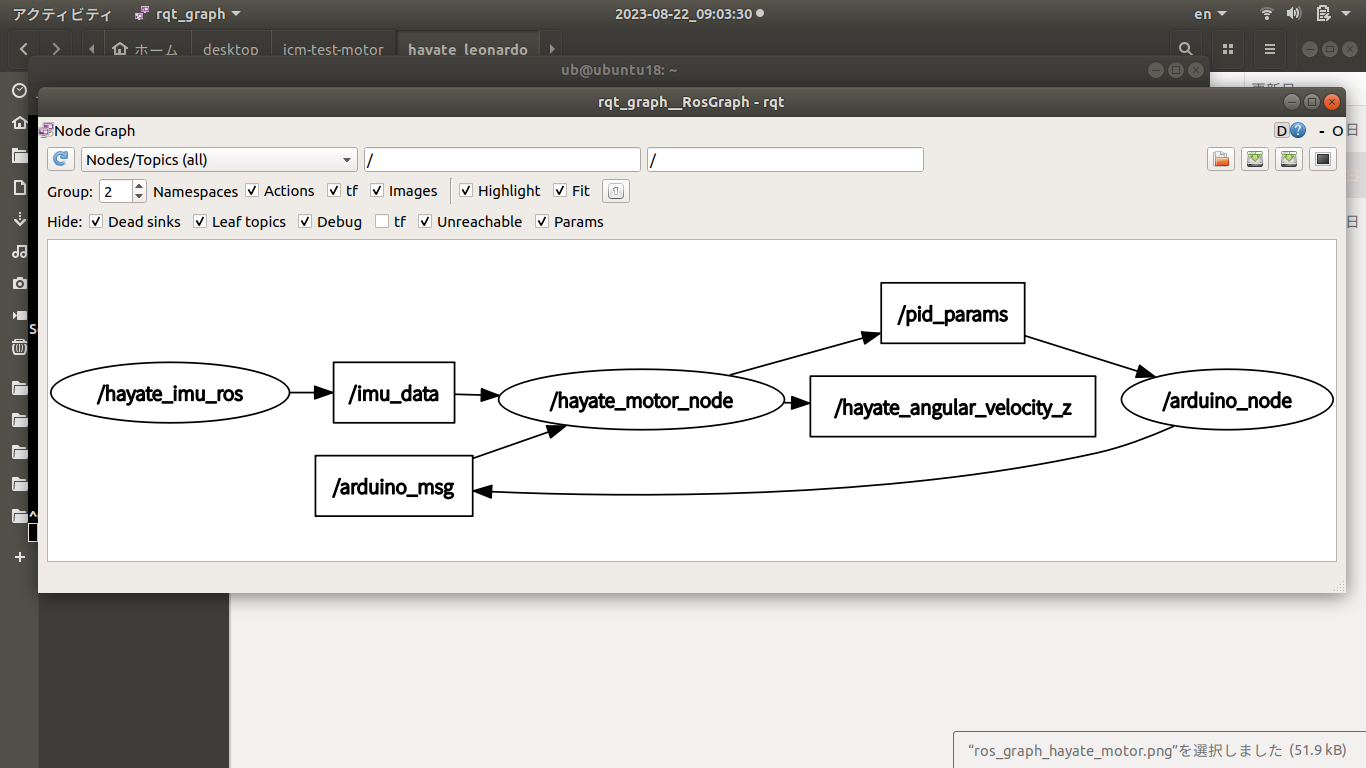
ROSノードの相互作用状況 エンコーダ付きDCモータPID制御の実験-ROS node & ROS topic Arduinoノード エンコーダA相パルス割込みハンドラ
if (digitalRead(ENCODER_A) != digitalRead(ENCODER_B)) {
current_counter++;
}
else {
current_counter--;
}
エンコーダB相パルス割込みハンドラ
if (digitalRead(ENCODER_A) == digitalRead(ENCODER_B)) {
current_counter++;
}
else {
current_counter--;
}
エンコーダカウンタによる回転速度
// Run the PID loop at 100 times per second
#define PID_RATE_HZ 10 // 10Hz
// Convert the rate into an interval
#define PID_INTERVAL_MS (1000 / PID_RATE_HZ) // 10ms
#define PID_INTERVAL_S (float)(1.0 / PID_RATE_HZ) // 0.1s
#define PPR 12 // Encoder pulse / round
#define COUNTER_FACTOR 4 // 1*encoder-pulse = 4*counter
#define REDUCTION_RATIO 100 // Gear reduction ratio
#define CPR (PPR * COUNTER_FACTOR * REDUCTION_RATIO) // Counters of encoder / round
current_velocity = (current_counter - previous_counter) * 360.0 / (CPR * PID_INTERVAL_S);
PID係数
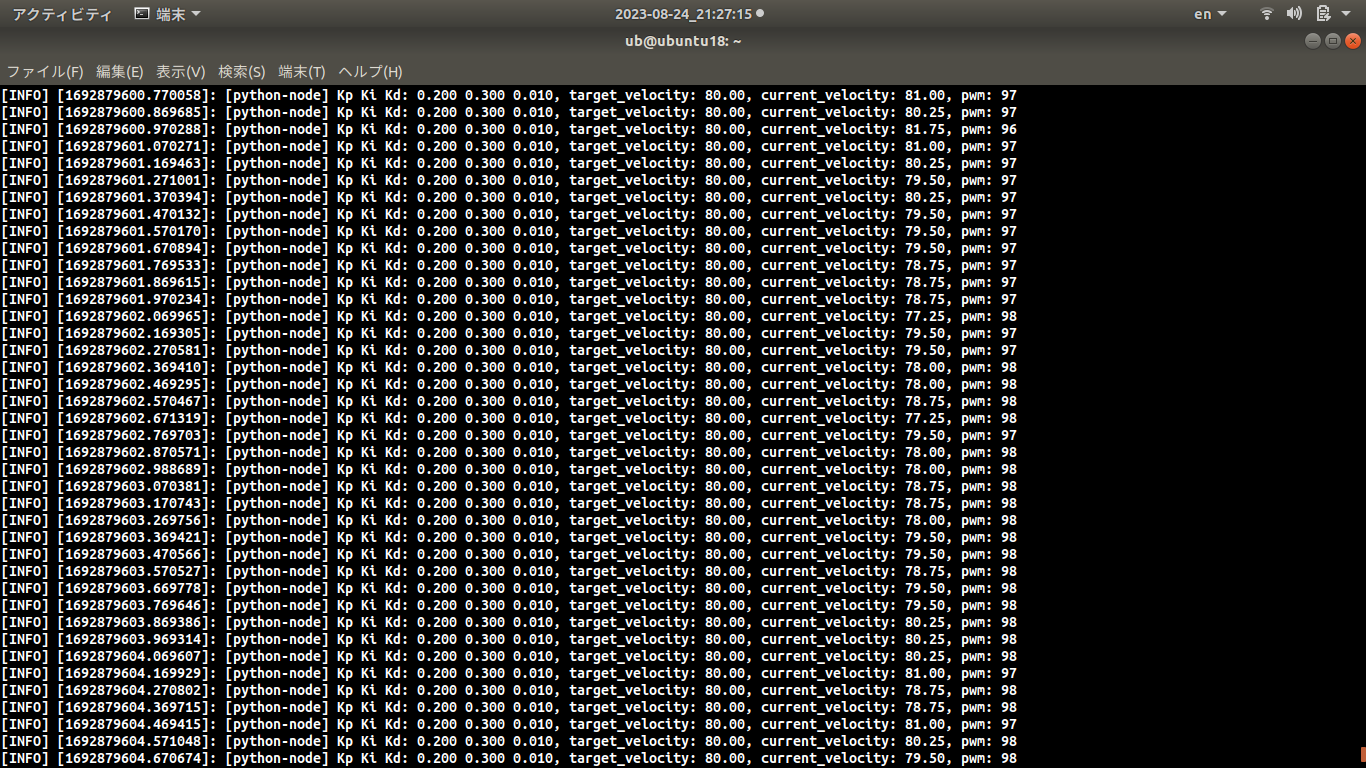
本実験環境で何回も実験を繰り返して、納得いくPID係数Kp、Ki、Kdを決めておく。
PID操作量
●Position法
error = target_velocity - current_velocity;
integral += error * PID_INTERVAL_S;
differential = (error - previous_error) / PID_INTERVAL_S;
previous_error = error;
pwm = (int32_t)(Kp * error + Ki * integral + Kd * differential);
●Increment法
error = target_velocity - current_velocity;
proportion = Kp * (error - previous_error);
integral = Ki * error * PID_INTERVAL_S;
differential = Kd * (error - 2 * previous_error + previous_error2) / PID_INTERVAL_S;
pwm += (int32_t)(proportion + integral + differential);
previous_error2 = previous_error;
previous_error = error;
実験手順 Run roscore Run roscore@ROS Master
roslaunch haya_imu_ros haya_imu.launch
Launch hayate_imu_node Launch hayate_imu_node@ROS Slave
roslaunch hayate_imu_ros hayate_imu.launch
Launch hayate_motor_node Launch hayate_motor_node@ROS Master
roslaunch hayate_motor_ros hayate_motor.launch
rqt_graph
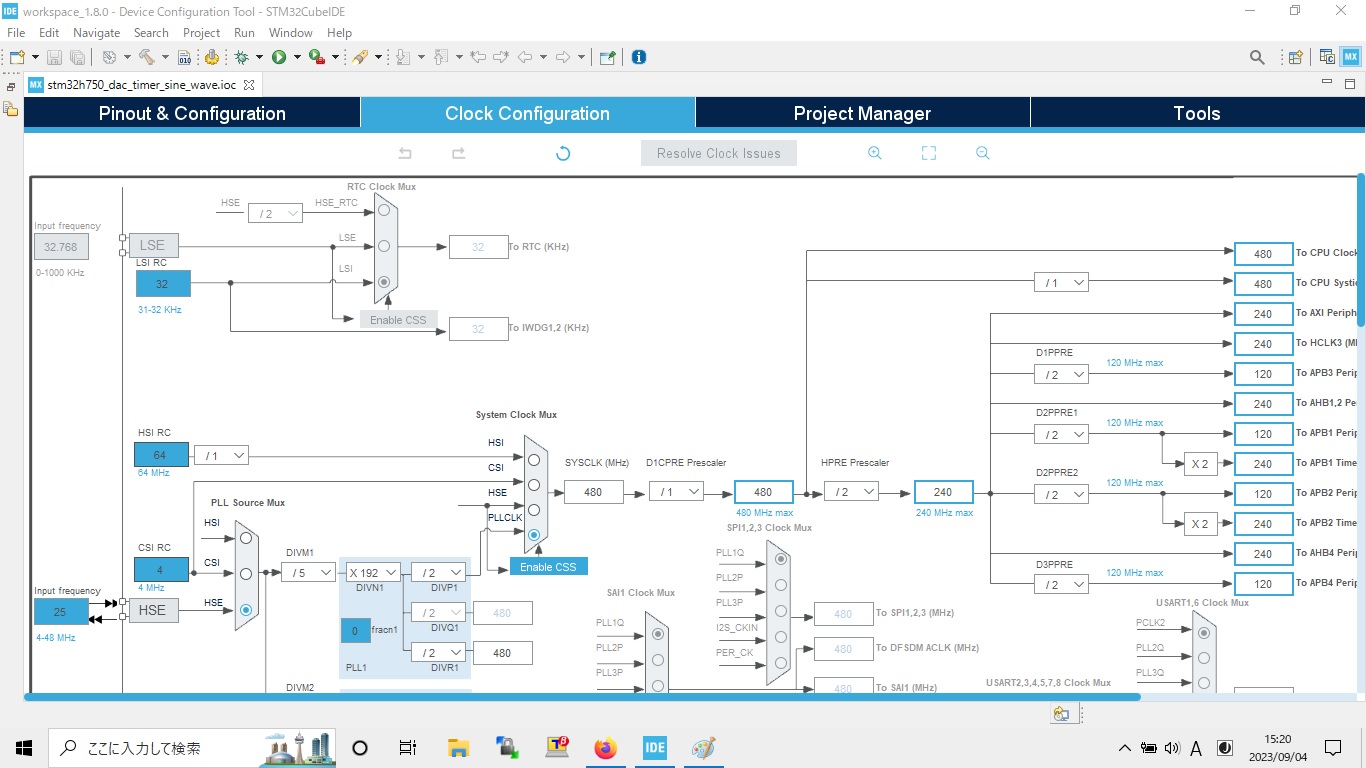
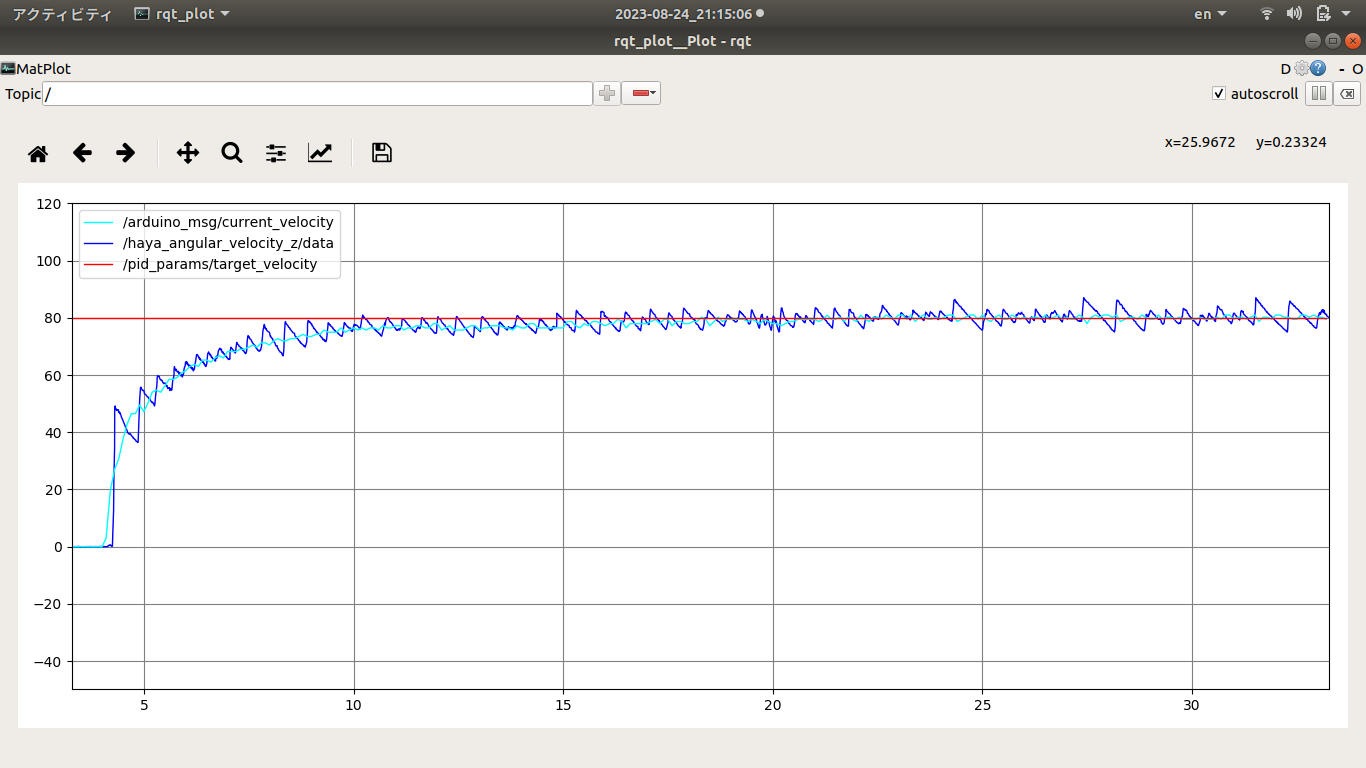
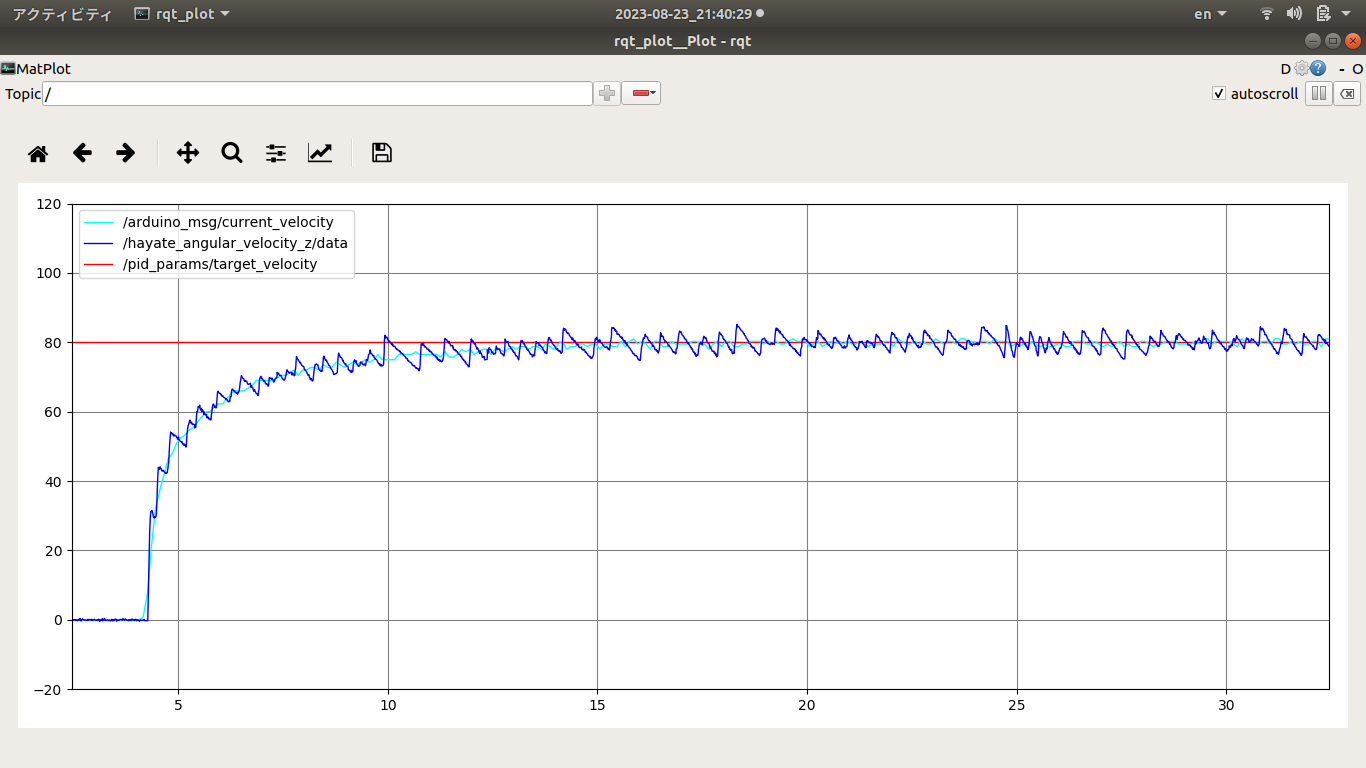
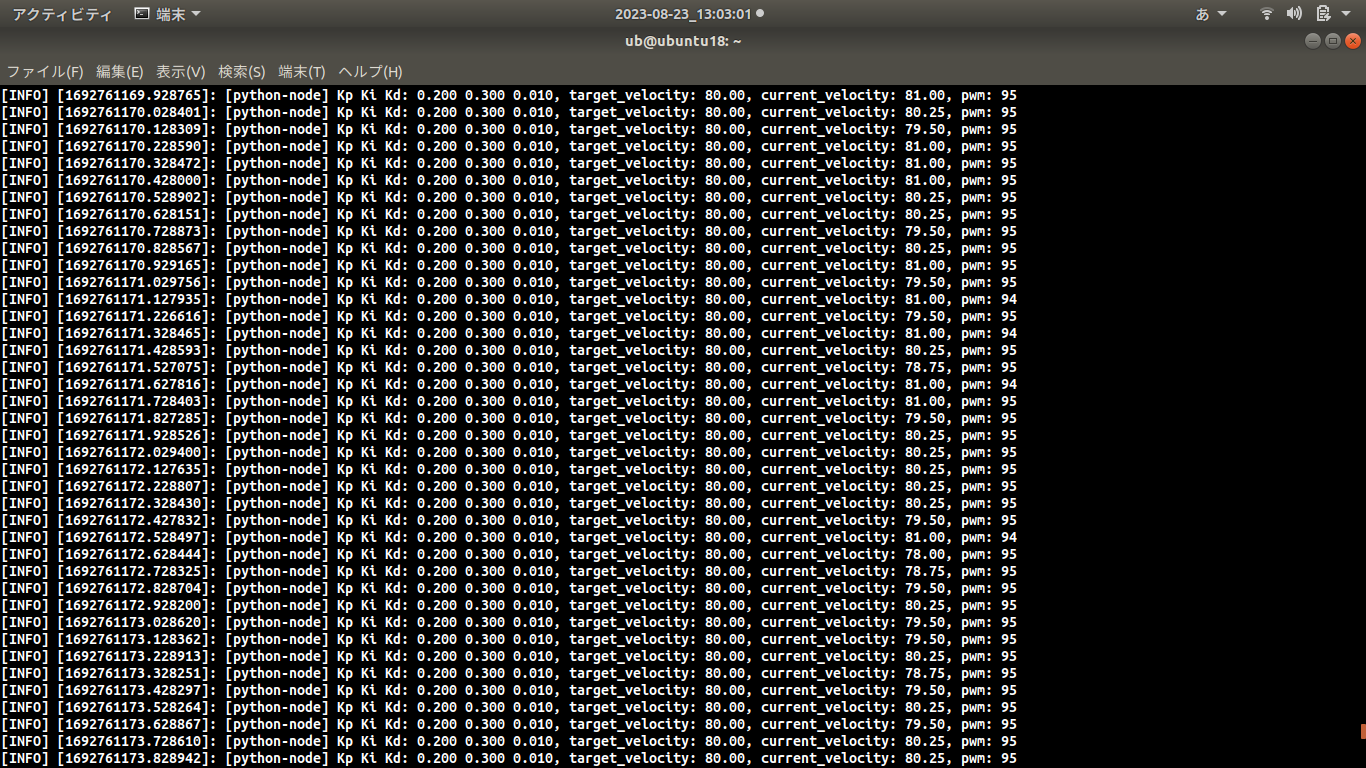
結果確認 PID制御の目標値、制御量 以下のデータを表示させて、エンコーダ、IMUからのカウンタによる回転速度を確かめて、PID係数Kp、Ki、Kdを決めてまた、エンコーダまたは、PID制御を評価する。PWM周波数をデフォルトの490Hzから4KHzに変更することで回転速度の分散は小さくなっている。これは490Hzより4KHz周波数のほうはモータにブレーキをかけずにPWM波形は滑らかになって果たしてモータ出力シャフトの回転速度も滑らかになったわけである。
/hayate_angular_velocity_z
/pid_params/target_velocity
/arduino_msg/current_velocity
PID制御の目標値、エンコーダによる回転速度、hayate_imu測った回転速度曲線 hayate_imuで測った回転速度が、エンコーダによる回転速度より分散が大きくなって、これは測定法および測定ポジションは違って、またモータシャフトによる振動や、慣性力に由来するものと考えられる。
PID制御の目標値、制御量、操作量 PID制御の目標値、PWM操作量、エンコーダによる回転速度PID制御の目標値、PWM操作量、エンコーダによる回転速度
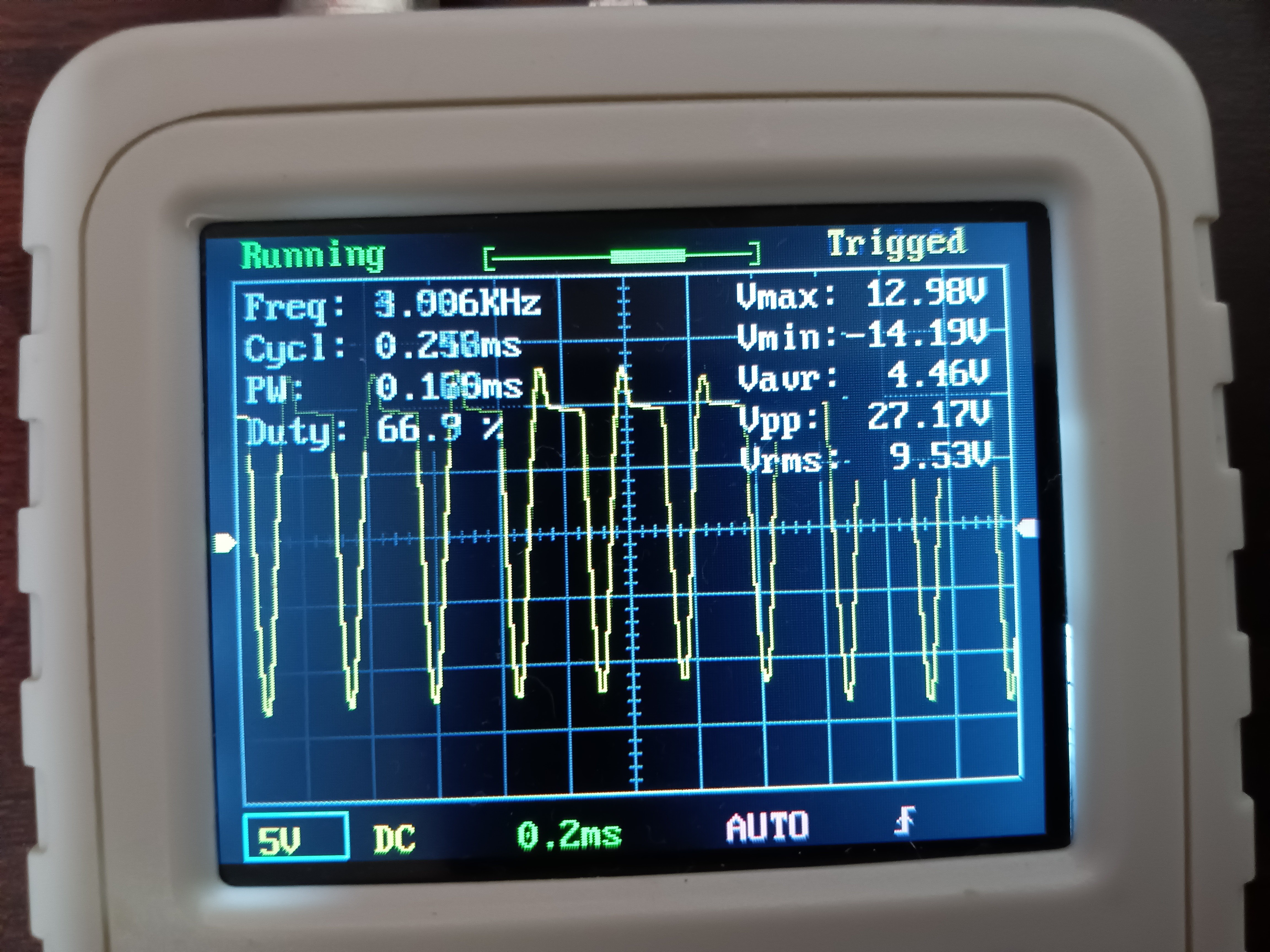
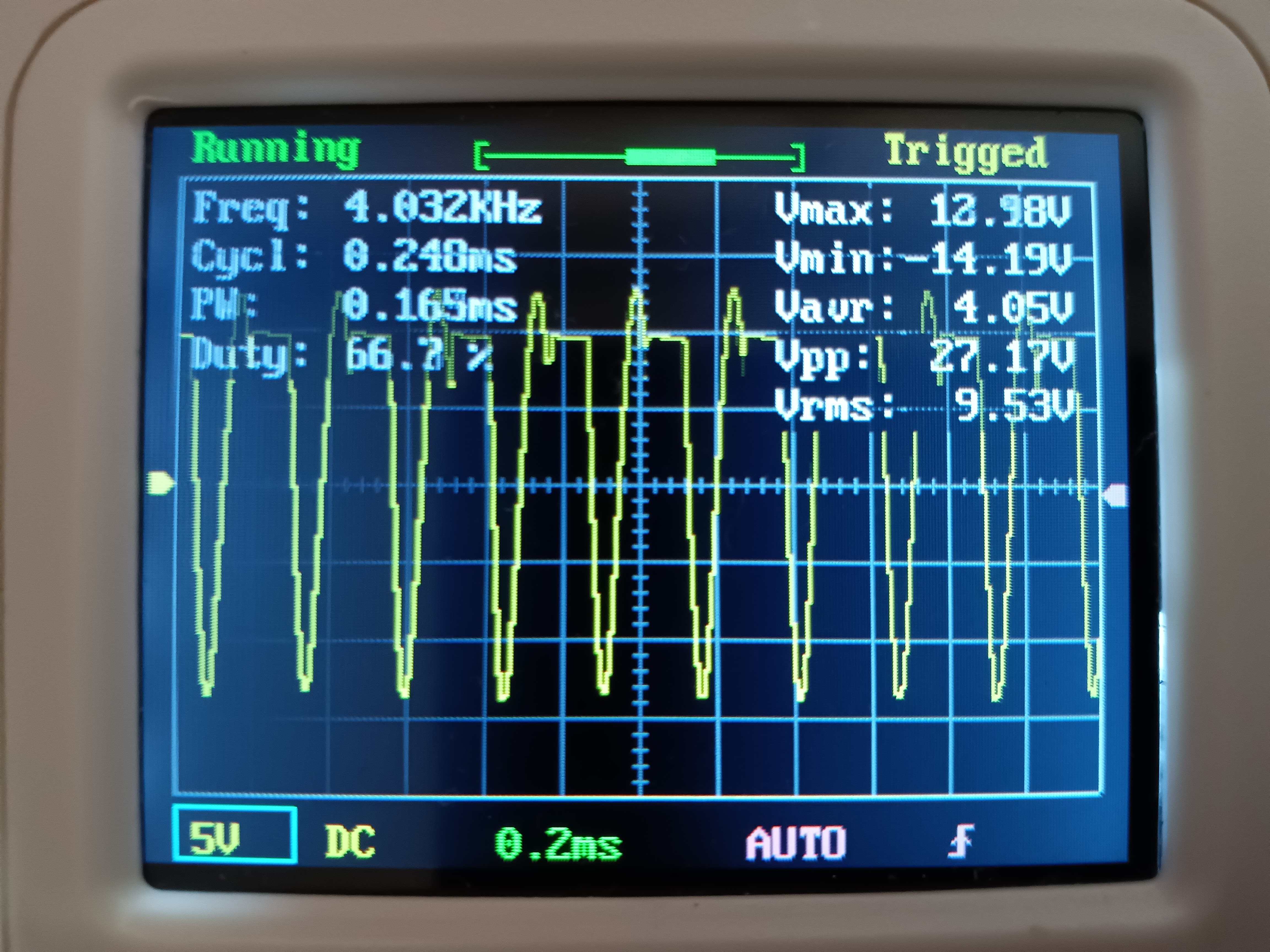
PID制御の操作量PWM波形 オシロスコープは測った操作量PWMの波形、モータコイルに起因する逆起電力による、コイルサージは約-14Vあったと、モータシールド実装モータドライバL293Dにコイルサージ(逆起電流)を流すダイオードが効いていると考えられる。ないと一瞬-12Vの数十倍~-1千万V(無限大)に達する可能性ある。これで回路で繋がっているデジタルICを一発でぶち壊すことになる。PID制御の操作量PWM波形
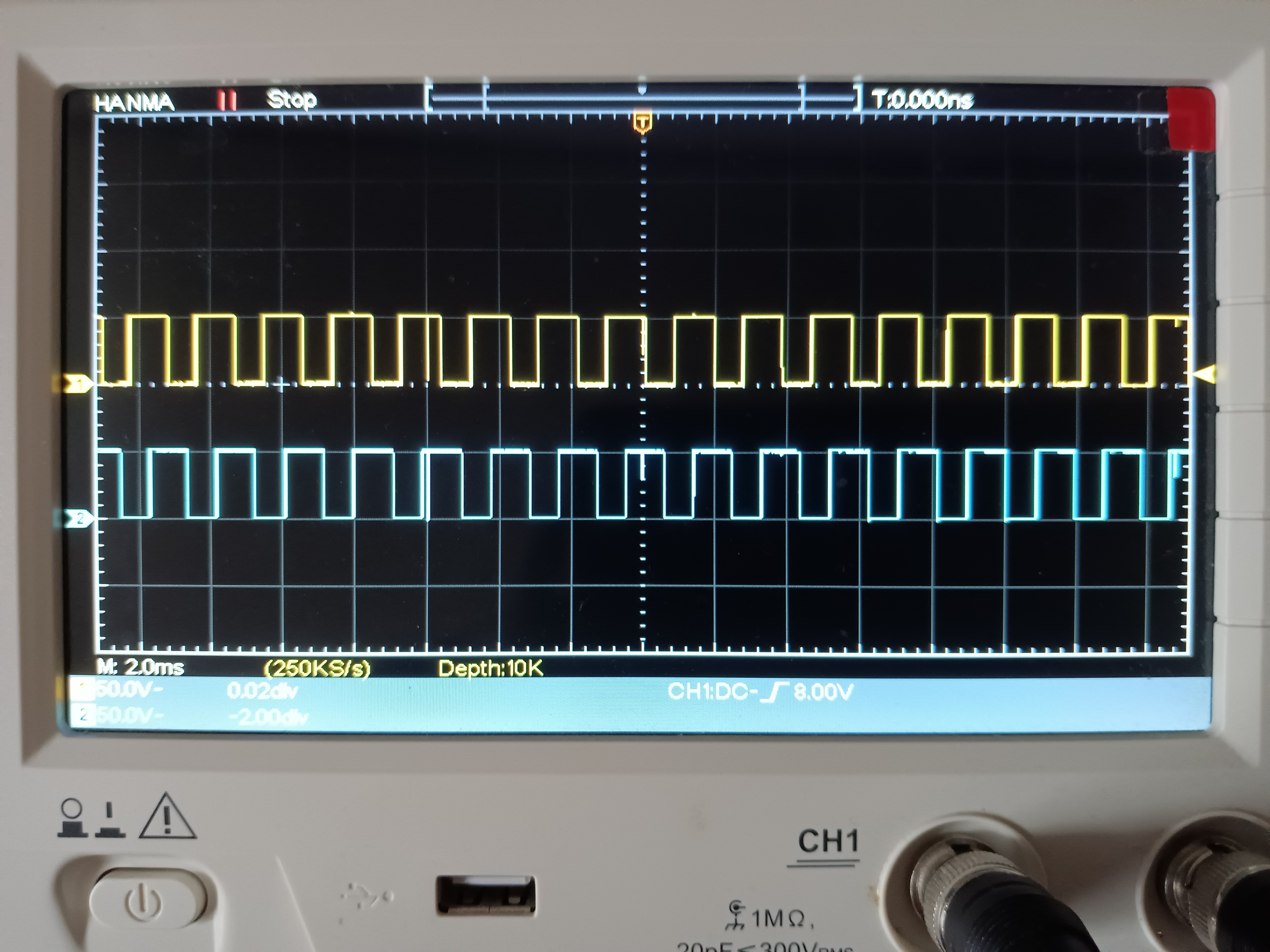
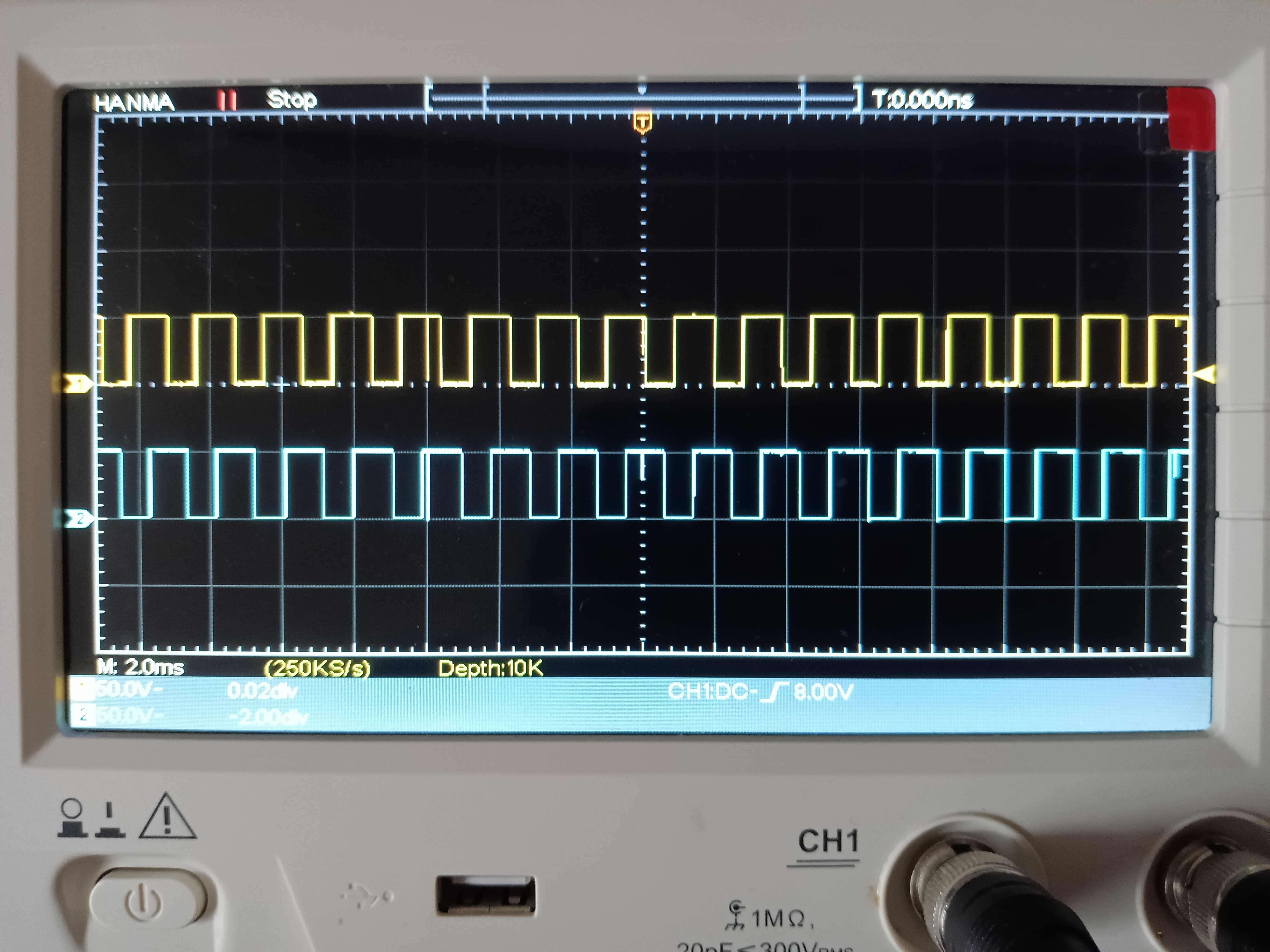
エンコーダ出力パルス波形 約1/10の確率でノイズに起因するスパイクが起きるらしいので、MCUにノイズフィルタ実装の入力PINは望ましい。エンコーダパルス波形ノイズスパイクあり
リポジトリ hayate_motor_ros、arduino_node、修正ありMotor Shieldライブラリ含むリポジトリは、https://github.com/soarbear/hayate_motor_ros に公開済み(BSD 3-Clause License)
最後に IMUはモータシャフトでなくロボット本体に装着した場合、エンコーダのみならずLidar、カメラ、GPS他のセンサーとフュージョンする場合多い。
参考記事 ●ロータリエンコーダによる速度計算 9軸IMUセンサ 6軸/9軸フュージョン 低遅延 USB出力 補正済み ROS対応
ロボット・ドローン部品