はじめに
教師あり学習\((Supervised \space Learning)\)は入力に正しい出力を与える学習に対して、強化学習\((Reinforcement \space Learning)\)は、試行錯誤を通じて環境に適応する学習である。強化学習メカニズムは、エージェント\((Agent)\)例えばニューラルネットワークが取得する累積報酬\((Reward=r)\)を最大化するための状態\((State=s)\)から行動\((Action=a)\)への方策\((Policy=\pi)\)を獲得する。強化学習に少ない学習データでタスクの遂行と深層学習に連携することから研究は盛んになっている。
\(MDP\)マルコフ決定過程
マルコフ決定過程\((Markov \space Decision \space Process=MDP)\)は、状態遷移が確率的に生じる動的システム(確率システム)の確率モデルであり、状態遷移がマルコフ性を満たすものをいう。マルコフ性とは状態\(s_{t+1}\)への遷移がそのときの状態と行動\((s_t,a_t)\)のみに依存するが、それ以前の状態や行動\((s_{t-1},a_{t-1})\)には関係ないこと。強化学習で時系列状態遷移の表現を簡略するマルコフ決定過程\(MDP\)を用いると、累積報酬\(r\)を最大化することを\(MDP\)が適用した価値関数を求めることに変わる。状態価値関数と状態-行動価値関数はベルマン方程式\((Bellman \space Euqation)\)による表現がある。
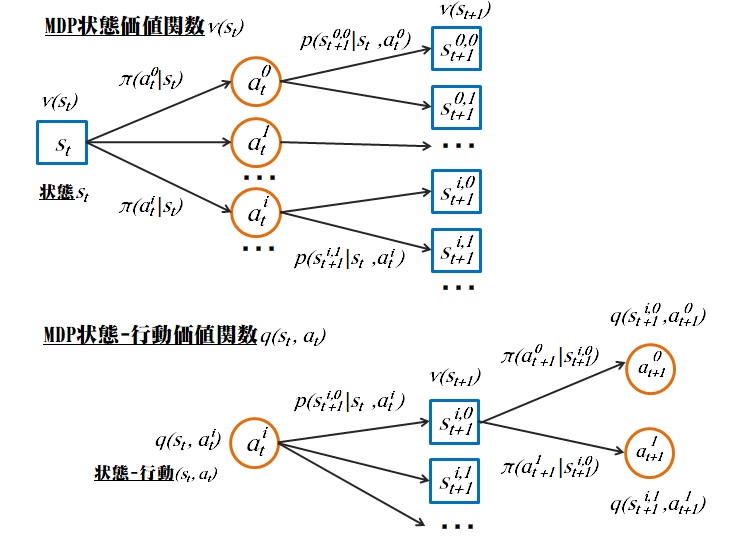
状態価値関数
図1から、次式の状態価値関数のベルマン方程式がまとまる。つまり状態価値\(v\)は割引(減衰)\(\gamma\)を考慮した報酬\(r\)の総和となる。
$$\small v_π(s_t)=\sum_{a_t} π(a_t|s_t) \sum_{s_{t+1}} p(s_{t+1}|s_t,a_t)[r_{a_t}^{s_{t+1}}+\gamma v_{\pi} (s_{t+1})]\space \space (1) $$
状態価値関数だけでは最適な方策(行動)が分からないので、状態-行動価値関数なら方策(行動)が分かる。
状態-行動価値関数
図1から、次式の行動価値関数がまとまる。つまり状態-行動価値\(q\)は割引(減衰)\(\gamma\)を考慮した報酬\(r\)の総和となる。
$$\scriptsize q_π(s_t,a_t)= \sum_{s_{t+1}} p(s_{t+1}|s_t,a_t)[r_{a_t}^{s_{t+1}}+ \gamma \sum_{a_{t+1}}π(a_{t+1}|s_{t+1})q_π(s_{t+1},a_{t+1})]\space \space (2) $$
図1から、状態価値関数と状態-行動価値関数の相互関係が分かる。
相互関係
$$v_π(s_t)=\sum_{a_t}π(a_t|s_t)q_π(s_t,a_t) \space \space (3) \\ \small
q_π(s_t,a_t)=\sum_{s_{t+1}}p(s_{t+1}|s_t,a_t)[r_{a_t}^{s_{t+1}}+\gamma v_π(s_{t+1})] \space \space(4)
$$
式(1)~(4)までを利用して累積報酬を最大化する方策を求めるには、方策反復法\((Policy \space Iteration)\)、価値反復法\((Value \space Iteration)\)、\(Q\)計画法\((Q-Planning)\)などがある。
方策反復法
全ての状態の報酬が変わらないほどまで、\(T\)回繰り返す。
$$\scriptsize v_{\pi}^{T}(s_t)=\sum_{a_t} π(a_t|s_t) \sum_{s_{t+1}} p(s_{t+1}|s_t,a_t)[r_{a_t}^{s_{t+1}}+\gamma v_{\pi}^{T-1} (s_{t+1})]\space \space (5) $$
全ての状態の報酬から最大の報酬を招く方策は最適方策\(\pi_*^{T+1}(s)\)である。
$$\small \pi_*^{T+1}(s)=\underset{a}{\operatorname{argmax}} \sum_{s_{t+1}}p(s_{t+1}|s_t,a_t)[r_{a_t}^{s_{t+1}}+\gamma v_π^T (s_{t+1})] \space \space(6) $$
なお最適方策\(\pi_*^{T+1}(s)\)を最大報酬\(v_*^{T+1}(s)\)に書き換えて価値反復法を表す(7)式となる。
価値反復法
$$\small v_*^{T+1}(s)=\underset{a}{\operatorname{max}}\sum_{s_{t+1}}p(s_{t+1}|s_t,a_t)[r_{a_t}^{s_{t+1}}+\gamma v_π^T (s_{t+1})] \space \space(7) $$
実装
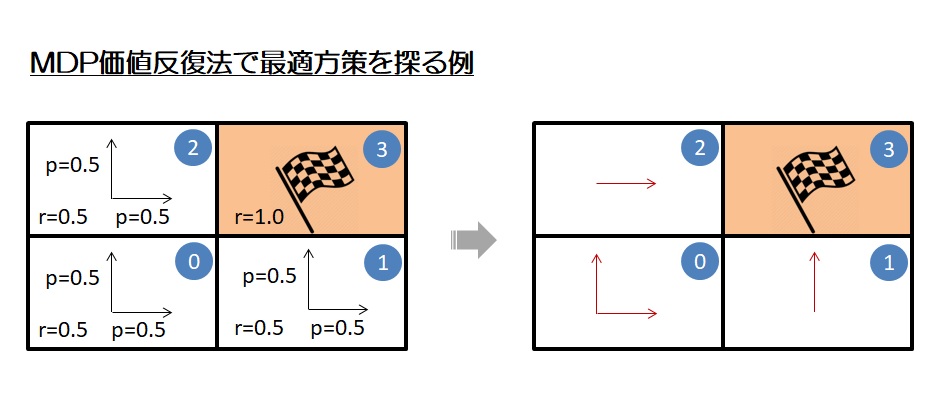
図2に格子4つ中の3つの最適方策を価値反復法の例として実装する。
#
# Title: The best policy calculated with MDP value itertation method
# Author: T.Yanagi
#
import numpy as np
import copy
#
# 価値反復法で3状態x2行動のMDPマルコフ決定過程を解く
#
def value_iteration():
# 行動の条件確率p[s(t+1)|s(t),a(t)]の設定
p = [0.5, 0.5, 0.5]
# 割引率γの設定
gamma = 0.90
# ループ終了判定基準係数の設定
epsilon = 0.001
# 報酬値r[s]の設定
r = [0.5, 0.5, 0.5, 1.0, 0.0]
# 価値関数r[s]の初期化
v = [0.0, 0.0, 0.0, 0.0, 0.0]
v_new = copy.copy(v)
# 状態-行動価値関数q(s,a)の初期化
q = np.zeros((3, 2))
# 方策分布(pi(s))の初期化
pi = [0.5, 0.5, 0.5]
# 状態s(t+1)の初期化 3x2
s_t1 = np.zeros((3, 2))
s_t1[0, 0] = 2 # up
s_t1[0, 1] = 1 # right
s_t1[1, 0] = 3 # up
s_t1[1, 1] = 4 # right(out)
s_t1[2, 0] = 4 # up(out)
s_t1[2, 1] = 3 # right
iteration = 0
# 価値反復法の計算
while True:
delta = 0.0
for i in range(3):
# 行動価値関数を計算
q[i, 0] = p[i] * (r[int(s_t1[i,0])] + gamma * v[int(s_t1[i,0])])
q[i, 1] = (1.0 - p[i]) * (r[int(s_t1[i,1])] + gamma * v[int(s_t1[i,1])])
# 行動価値関数のもとで greedy に方策を改善
if q[i, 0] > q[i, 1]:
pi[i] = 1
elif q[i, 0] == q[i, 1]:
pi[i] = 0.5
else:
pi[i] = 0
# 改善された方策のもとで価値関数を計算
v_new = np.append(np.max(q, axis=-1), [0.0, 0.0])
# 現ステップの価値関数と方策を表示
print(f'iteration: {iteration}, value: {v_new[:3]} policy: {pi}')
delta = max(delta, abs(np.min(v_new[:3] - v[:3])))
# 計算された価値関数 v_new が前ステップの値 v を改善しなければ終了
if delta <= epsilon * (1 - gamma) / gamma:
# 最適方策を返す
return pi
# 価値関数を更新
v = copy.copy(v_new)
iteration += 1
#
# main()
#
if __name__ == '__main__':
# 価値反復法最適方策を探る
pi = value_iteration()
# 行動方向表示の初期化
direction = ['','','']
# 最適方策を表示
for i in range(3):
if pi[i] == 1.0:
direction[i] = '^'
elif pi[i] == 0.5:
direction[i] = 'L'
else:
direction[i] = '>'
print(f'{direction[2]} 0\n{direction[0]} {direction[1]}')
ソースコード
https://github.com/soarbear/Reinforcement_Learning
実行
以下の結果は図2の右にある結果の部分に合致するのを分かる。
iteration: 0, value: [0.25 0.5 0.5 ] policy: [0.5, 1, 0] iteration: 1, value: [0.475 0.5 0.5 ] policy: [0.5, 1, 0] > 0 L ^
参考文献
[1]現場で使える!Python深層強化学習入門、翔泳社
[2]Reinforcement Learning: An Introduction. by Richard S.Sutton, Andrew G.Barto.