はじめに
wiki: 「カルマンフィルタ\((Kalman Filter, KF\)と略す\()\) は、誤差のある観測値を用いて、ある動的システムの状態を推定あるいは制御するための、無限インパルス応答フィルタの一種である」。観測値に観測雑音、状態予測値にシステム雑音があって場合により時間とともに誤差がドンドン蓄積してそのまま使えないので、観測と予測のガウス性を利用した線形センサデータフュージョンがカルマンフィルタの原点である。
状態空間モデル
時系列解析の中で、予測値と観測値の間何らかの因果関係を見つけて、何らかの方法でそれらのデータを絡んでモデル化して状態を推定していく。ここで汎用的な状態方程式、観測方程式は以下の式にする。
$$\begin{eqnarray*}&& x_t = F_{t-1}(x_{t-1} ) + q_{t-1}\\&& y_t = H_t(x_t) + r_t\end{eqnarray*}$$
ただし、システム雑音、観測雑音\((q_t, r_t)\)は期待値が\(0\)、分散が\((Q_t, R_t)\)の独立正規分布(ガウス分布)にする。
$$\begin{eqnarray*}&& p(q_t) ~ N(0,Qt)\\&& p(r_t) ~ N(0,Rt)\\&& E[q_t r_t]=0 \end{eqnarray*}$$
基本原理
カルマンフィルタの原理は以下のイメージに示すように、最小解析誤差推定(最小二乗)から予測値、観測値をそれぞれの割合\(I-K_t H_t , K_t\)で線形合成した値を状態推定値にする。
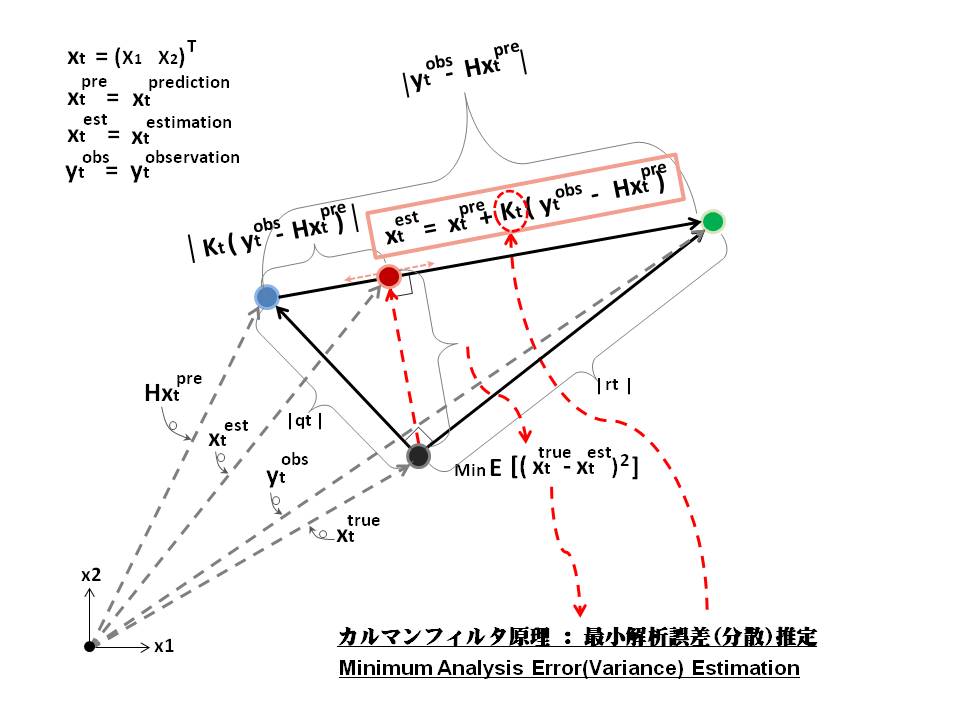
式の導出
ベイズの定理やガウス分布からいくつかのの導出方法はあるが、本記事はシンプルな最小二乗法からカルマンフィルタの黄金\(5\)式\(\space *\)を誘導する。
線形システム
\(F(.),H(.)\)とも線形関数の場合、以下線形カルマンフィルタの誘導となる。例えば\( F(x)=Ax+B\)、\(A,B\)とも実数行列、\(x\)は変数行列とする。
まずは、予測値(数学期待)を求めるのは出発点なので、すべては以下の式から始まる。
$$ \gamma_t = F_{t-1}(\gamma_{t-1}) \space \space c $$
推定値\(x_t^{est}\)は、重み\(K_t\)の調整で予測値\(x_t\)と観測値\(y_t\)の間にあろうとして、以下線形表現がある。
$$ x_t^{est} = x_t + K_t(y_t-H_t x_t) \\
{\small = F_{t-1}(x_{t-1}^{true}+p_{t-1}) + q_{t-1}+ K_t\{(H_t x_t^{true}+r_t) }\\
{\small – H_t(F_{t-1}(x_t^{true}+p_{t-1})+q_{t-1})\} }\\
{\scriptsize = x_t^{true}+F_{t-1}p_{t-1}+q_{t-1}+K_t(r_t-H_t F_{t-1}p_{t-1}-H_t q_{t-1}) }$$
解析誤差(共分散\(P_t\))は以下の式より求める。
$$ P_t = E[(x_t^{est}-x_t^{true})^2] \space \space \\
{\scriptsize = E[(F_{t-1}p_{t-1} + q_{t-1} + K_tr_t-K_t H_t F_{t-1}p_{t-1}-K_t H_t q_{t-1})^2] }\\
{\scriptsize = F_{t-1}P_{t-1}F_{t-1}^T-2F_{t-1}P_t F_{t-1}^TH_t^T K_t^T+Q_{t-1}-2Q_{t-1}H_t^T K_t^T }\\
{\scriptsize + K_t R_t K_t^T+K_t H_t F_{t-1}P_{t-1}F_{t-1}^TH_t^T K_t^T+K_t H_t Q_{t-1}H_t^T K_t^T } $$
ここから二乗の最小化より解析誤差(共分散\(P_t\))を最小値に至らせる\(K_t\)を求める。
$$ \frac {\partial P_t } {\partial K_t } = 0 \\
{\small \frac {\partial P_t } {\partial K_t } = -2F_{t-1} P_{t-1} F_{t-1}^T H_t^T -2Q_{t-1}H_t^T } \\
{\small +2K_t R_t + 2K_t H_t F_{t-1} P_{t-1} F_{t-1}^T H_t^T +2K_tH_tQ_{t-1}H_t^T } \\
{\small K_t = (F_{t-1}P_{t-1}F_{t-1}^T + Q_{t-1}) H_t^T \{R_t } \\
{\small + H_t(F_{t-1}P_{t-1}F_{t-1}^T+Q_{t-1})H_t^T\}^{-1} } $$
これで、状態予測時\( K_t = 0 \)より、式\(\cdot\)を\({\small P_t = F_{t-1}P_{t-1}F_{t-1}^T + Q_{t-1} \space ** }\)に、\( K_t\)は、以下のように簡略化する。
$$ K_t = P_t H_t^T (R_t + H_t P_t H_t^T)^{-1} \space \space *** $$
これから観測値を入れて、\(K_t\) を使って推定値を求める。
$$ x_t^{est} = x_t + K_t(y_t – H_t x_t) \space \space **** $$
推定値を求めたら、続いて\(P_t\)を更新する。前述した\(#\)式の展開の項らより、最後の式は誘導できる。
$$ P^{\prime}_t = (I – K_t H_t)P_t \space \space ***** $$
\(P^{\prime}_t\)は、\((t+1)\)時刻の\(P_t\)として利用される。
非線形システム
線形カルマンフィルタの\(F(.),H(.)\)は非線形関数の場合、\(f(.),h(.)\)と記す。例えば\(f(x)=Ax^2+B\)、\(A,B\)とも実数行列、\(x\)は変数行列として、ティラー展開の最初の\(2\)項のみ使って、\( \hat{f}(x)=f(a)+\frac {\partial {f(x)}} {\partial {x}}|_{x=a}x \) のように\(Aa^2+B+2A(Aa^2+B)x\)に線形化することができる。\(3\)項目以降は捨てるので大いに誤差を招く可能性ある。状態予測の際に線形カルマンフィルタの\(F\)を\(f\)、観測値の取り入れる際に線形カルマンフィルタの\(H\)を\(h\)に、共分散行列の計算の際に\(F,H\)を\( \frac {\partial {f(x)}} {\partial {x}}|_{x=x_{t-1}}, \frac {\partial {h(x)}} {\partial {x}}|_{x=x_t}\)に置き換えて済む。
これまでカルマンフィルタの誘導で、状態値推定の手順を以下のとおり整理しておく。
推定の手順
時系列の状態推定に応用して、以下状態予測\(Predict\)→測定更新 \(Measurement \space Update\)→状態更新\(Correct, Update\)→時間更新\(Time \space Update\)→次の状態予測\(Predict\)→\(…\)の繰り返すことによって、時系列とともに状態の数学期待と最小解析誤差(共分散)を求める手順となる。
Step0=パラメータ初期化(t=0)
状態推定(数学期待)、解析誤差共分散の初期化
$$\begin{eqnarray*}&& \hat{x}_0 = E[x_0]\\&& \hat{P_0} = E[(x_0-\hat{x_0})(x_0-\hat{x_0})^T]\end{eqnarray*}$$
Step1=状態値、共分散行列予測(t>0)
$$\begin{eqnarray*}&& \bar{x_t} = F_{t-1}(\hat{x}_{t-1})\\&& \bar{P_t} = F_{t-1}\hat{P}_{t-1}F_{t-1}^T + Q_{t-1}\end{eqnarray*}$$
ただし、\(\bar{x_t}\)は予測値、\(\bar{P_t}\)は事前共分散行列、\(Q_{t-1}=E[q_{t-1}q^T_{t-1}]\)
Step2=カルマンゲイン、状態値、共分散行列更新
$$\begin{eqnarray*}&& K_t = \bar{P_t}H_t^T(H_t\bar{P_t}H_t^T + R_t)^{-1}\\
&& \hat{x_t} = \bar{x_t} + K_t(y_t – H_t\bar{x_t})\\&&\hat{P_t} = (I-K_tH_t)\bar{P_t} \end{eqnarray*}$$
ただし、\(K_t\)はカルマンゲイン、\(\hat{x_t}\)は状態推定値、\(\hat{P_t}\)は事後共分散行列、\(R_{t}=E[r_{t}r^T_{t}]\)
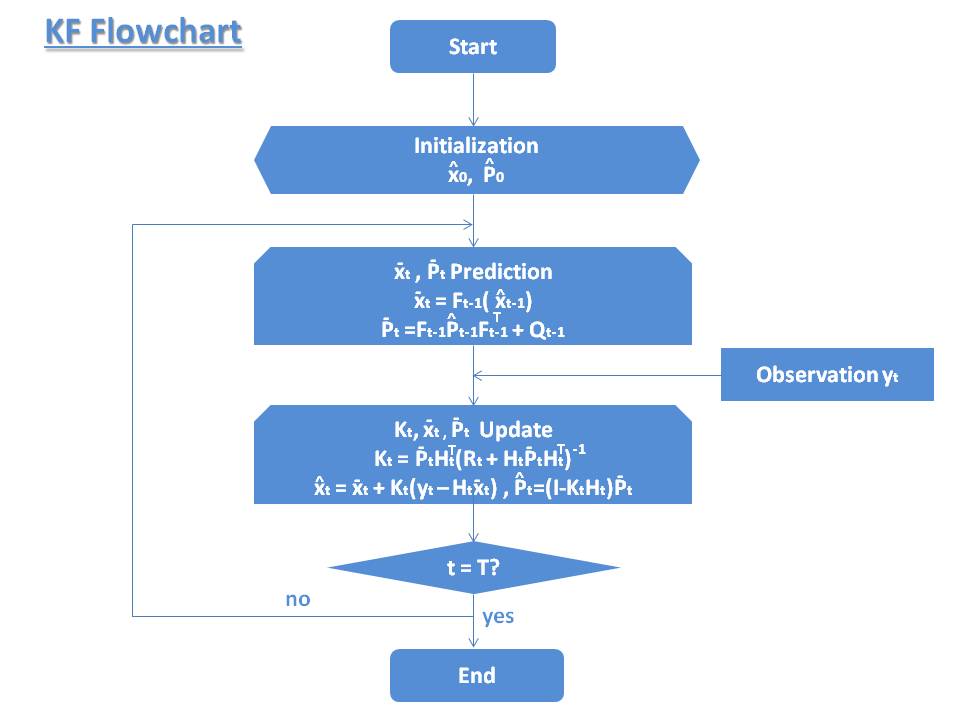
KFフローチャート
拡張カルマンフィルタ
拡張カルマンフィルタ\((Extended Kalman Filter, EKF\)と略す\()\)は、非線形フィルタリングである。前述した状態方程式、観測方程式より、以下の状態空間モデルの\(f(⋅)\)または\(h(⋅)\)が非線形関数であり、拡張カルマンフィルタが適用される。テイラー展開より、2次微分以降の項目を省略して、非線形である\(f(⋅), h(⋅)\)の1次微分を線形化とし、前述したカルマンフィルタのアルゴリズムが適用可能となる。しかし、\(f(⋅), h(⋅)\)の微分では\(f(⋅), h(⋅)\)の一部しか表現できず、この線形化処理(1次微分)が誤差を大きく招く可能性がある。
$$\begin{eqnarray*}&& F_{t-1} =\frac{\partial f_{t-1}(x)}{\partial x}|_{x=\hat{x}_{t-1}}\\&& H_{t} =\frac{\partial h_{t}(x)}{\partial x}|_{x=\hat{x}_{t}}\end{eqnarray*}$$
状態空間モデル
$$\begin{eqnarray*}&& x_t = f_{t-1}(x_{t-1}) + q_{t-1}\\&& y_t = h_t(x_t) + r_t\end{eqnarray*}$$
Step0=パラメータ初期化(t=0)
$$\begin{eqnarray*}&& \hat{x}_0 = E[x_0]\\&& \hat{P_0} = E[(x_0-\hat{x_0})(x_0-\hat{x_0})^T]\end{eqnarray*}$$
Step1=状態値、共分散行列予測(t>0)
$$\begin{eqnarray*}&& \bar{x_t} = f_{t-1}(\hat{x}_{t-1})\\&& \bar{P_t} = F_{t-1}\hat{P}_{t-1}F_{t-1}^T + Q_{t-1}\end{eqnarray*}$$
ただし、\(\bar{x_t}\)は予測値、\(\bar{P_t}\)は事前共分散行列、\(Q_{t-1}=E[q_{t-1}q^T_{t-1}]\)
Step2=カルマンゲイン、状態値、共分散行列更新
$$\begin{eqnarray*}&& K_t = \bar{P_t}H_t^T(H_t\bar{P_t}H_t^T + R_t)^{-1}\\
&& \hat{x_t} = \bar{x_t} + K_t(y_t – h_t\bar{x_t})\\&&\hat{P_t} = (I-K_tH_t)\bar{P_t} \end{eqnarray*}$$
ただし、\(K_t\)はカルマンゲイン、\(\hat{x_t}\)は状態推定値、\(\hat{P_t}\)は事後共分散行列、\(R_t=E[r_t r^T_t]\)
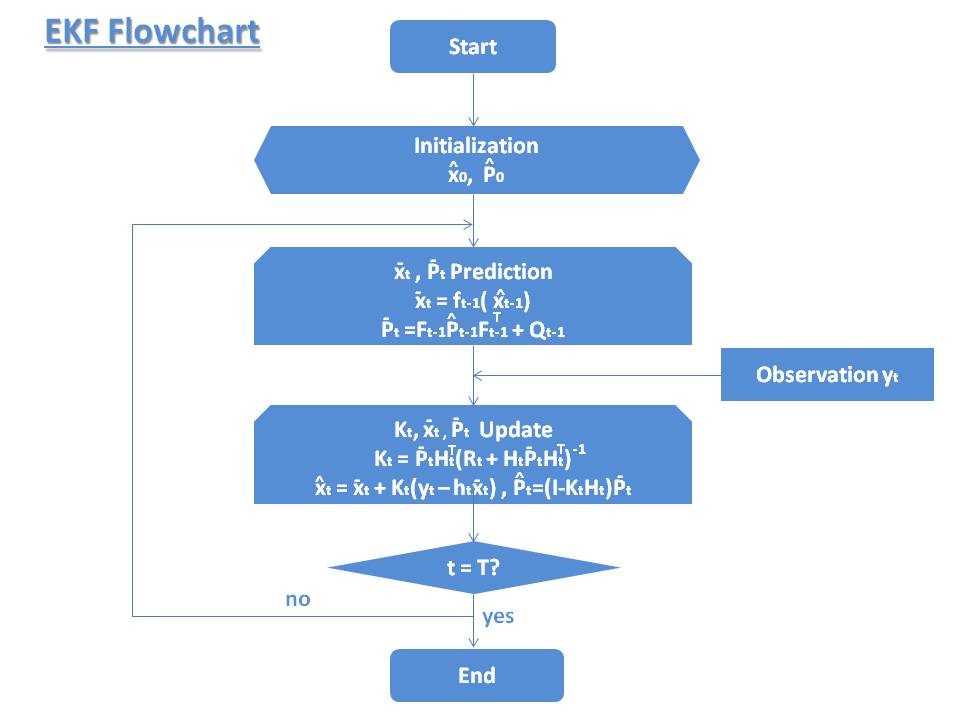
EKFフローチャート
拡張カルマンフィルタを6軸IMUへの適用
6軸IMUへの適用例として、本サイトの記事 6軸IMU~拡張カルマンフィルタ に載ってある。
カルマンフィルタの再考
カルマンフィルタでは、状態推定値を予測結果\(x_t\)(実装例ではジャイロセンサーデータ)と観測データ\(y_t\)(実装例では加速度センサデータ)の線形結合で合成し,その誤差を最小にする推定法だと分かる。これはシステム誤差、観測誤差の数学期待が0の正規分布との前提条件から由来した推定法である。しかし、カルマンフィルタをかけることで、状態推定値は予測結果と観測データの間にあるのは、真値からかなり乖離してしまう場合にあるのか。これはシステム誤差と観測誤差が無相関かつ直交という前提から、勿論真値が推定値と観測値の間にある結論を結ぶ考えである。また、ジャイロセンサーデータと、加速度センサデータとも観測値\(y_t\)にする方法がある。それぞれのパーフォーマンスの検証は、比較的精確な実験環境(比較用の高精度ジャイロセンサ、加速度センサ、エンコーダ、モータ)がないと、実は容易ではない。というよりも、シミュレーションをかけてカルマンフィルタのアルゴリズムを検証するのが、確実に可能である。
参考文献
1-wikipedia: カルマンフィルタ、オイラー角
2-Greg Welch氏、Gary Bishop氏: An Introduction to the Kalman Filter
3-田島洋氏: マルチボディダイナミクスの基礎―3次元運動方程式の立て方
関連記事
オイラー角~ジンバルロック~クォータニオン
SLAM~拡張カルマンフィルタ
SLAM~Unscentedカルマンフィルタ
9軸IMUセンサ 6軸/9軸フュージョン 低遅延 USB出力 補正済み ROS対応
9軸IMU ICM-20948をロボットに組み込もう
YDLIDAR G4=16m 薄型 ROS対応SLAM LIDAR
研究開発用 台車型ロボット キット