カテゴリー: 確率ロボティックス

9軸センサーICM-42688+MMC5983 6軸&9軸回転ベクトル&3軸オイラー角 MAX1000Hz同時出力 ROS/ROS2対応 USB接続

はじめに

令和3年度発売の旧型機種のhayate_imu v2は多くの企業、学校法人のユーザー様にご利用いただいたことに、厚く御礼申し上げます。ありがとうございます。旧機種はv2.4までとリリースさせていただいておりますが、いまユーザー様のお手元にある旧バージョン製品のファームバージョンアップは、ユーザー様のもとで実施可能なので、詳細については、別途順次ご案内申し上げます。昨今の半導体ショックにより供給不足、価格高騰などの影響を受ける中、後継機種の開発を続けてきた結果、令和5年4月下旬より、9軸IMU/AHRS haya_imu v3.2の発売をお知らせさせていただきます。

製品紹介

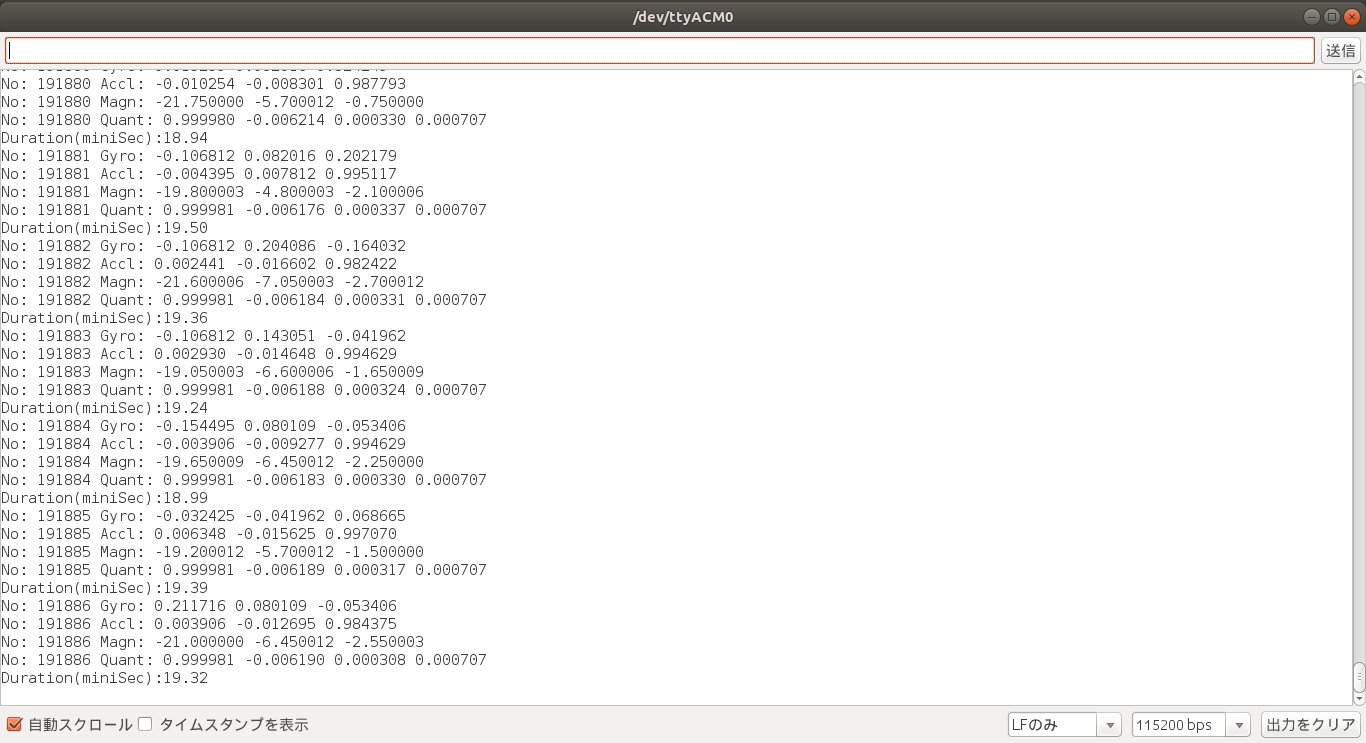
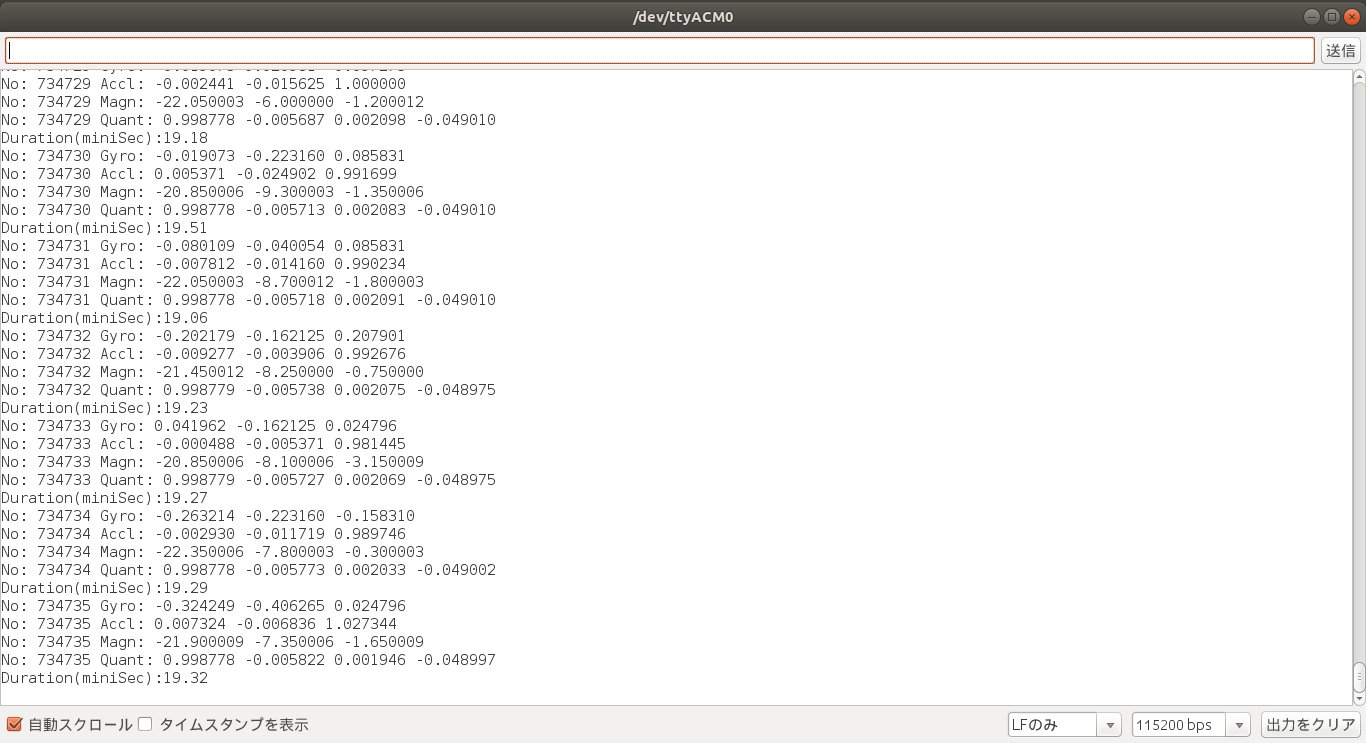
Cortex-M4 (クロック周波数120MHz)、新型6軸IMUのICM-42688、高精度3軸AMR方式地磁気センサMMC5983MAの実装により、通常出力モード、デモストレーションモード、キャリブレーションモード（初期バイアス測定）、6軸フュージョン回転ベクトルクォータニオン、9軸フュージョン回転ベクトルクォータニオン、3軸オイラー角の同時出力は最大1000Hzまで可能となります。ROS／ROS2とも対応しており、ドライバーはGithubよりダウンロードして製品とセットでご利用いただけます。

主な仕様

・型番　haya_imu v3.x
・内蔵チップ　Microchip Cortex-M4(120MHz)、ICM-42688-VまたはICM-42688-P、MMC5983MA実装
・外部接続　USB2.0+ Type-C、USB+5V給電
・最大出力レート
　　-　6軸/9軸フュージョン回転ベクトル四元数　1000Hz
　　-　3軸オイラー角　　1000Hz
　　-　3軸加速度(アクセル)データ　　1000Hz
　　-　3軸角速度(ジャイロ)データ　　1000Hz
　　-　IMU内部温度データ　　　　　　1000Hz
　　-　3軸地磁気(コンパス)データ　　500Hz

・測定レンジ
　　-　加速度(アクセル)センサ　　±8g
　　-　角速度(ジャイロ)センサ　　±2000dps
　　-　地磁気(コンパス)センサ　　±800µT

・バイアス測定補正　初期バイアス測定、動作時即時測定、内蔵補正機能あり
・消費電力　150mW以下(環境温度21℃ 実測値)
・寸法　38.0mm × 39.0mm × 4.8mm(突起物含む)
・取付穴　M3x4、隣り合う穴の中心間距離32.0mm

主な特長

・サービスモード　通常出力モード、デモンストレーションモード、キャリブレーションモード
・結果出力　6軸フュージョン回転クォータニオン、9軸フュージョン回転クォータニオン、3軸オイラー角1KHzまで同時出力、結果出力レートに関わらずIMU/地磁気センサのデータサンプリング周波数、フュージョン周波数は常に1000Hz/500Hzに設定済み
・初期バイアス測定　使用環境変化あった際に利用可能なキャリブレーションモードで最短数分程度で初期バイアス測定完了、MCUフラッシュに自動的に保存して、動作時に読み込んで即時バイアス測定＆補正あり
・地磁気センサ温度補償　地磁気センサは、計測時間1msにわたるセットリセット計測(温度補償機能)使用済み
・磁気外乱による干渉　受けにくいことが当社実験(磁束密度約2G)にて確認済み
・ROS/ROS2対応　本体にはROS/ROS2ライブラリを実装せず、対向装置にドライバーインストールにより実現

詳細情報

【製品名称】haya_imu v3.x
【開発会社】ROBOT翔（株式会社翔雲）
【発売時期】令和5年4月下旬頃
【商品情報】9軸センサー6軸&9軸回転ベクトル 3軸オイラー角 MAX1000Hz同時出力 ROS/ROS2対応 USB接続 | ROBOT翔

参考情報

エンコーダ付きDCモータPID制御の実験-haya_imu応用例

2+

ロボット・ドローン部品お探しなら
ROBOT翔・電子部品ストア

9軸IMUセンサ 6軸／9軸フュージョン 低遅延 USB出力 補正済み ROS対応

V2.4 NEWフィーチャ

令和5年3月、hayate_imu v2.4リリース!
較正モードの追加により、ジャイロスコープ、加速度センサ、地磁気センサの初期バイアスは出荷時の測定のみならず、ユーザー様のもとでも測定することはできる。 ※ いまユーザー様のお手元にある旧バージョン製品のファームウェアのバージョンアップは、ユーザー様のもとで実施可能なので、詳細については、別途順次ご案内する。

はじめに

9軸IMU(型番hayate_imu)は、コロナ禍の中で開発した新商品、令和3年3月まで開発～製造、令和3年4月上旬の出荷と予定して、皆さんの学術研究にお役に立てるようと願って、どうぞご検討ご利用のほど宜しくお願い申し上げます。

製品紹介

9軸センサhayate imu、低消費電力プロセッサーCortexM0+、TDK MPU-9250後継機種である、1.71V低電圧で動作可能なICM-20948使用、6軸／9軸融合クォータニオン(四元数)はFPGA on chip(DMP3)から低遅延出力、別途ソフトでフュージョン必要なし、最大出力レート225Hz、同時に加速度(アクセル)3軸データ225Hz、角速度(ジャイロ)3軸データ225Hz、地磁気(コンパス)3軸データ70Hzまで出力可能、補正済み、ROS対応。ロボット、ドローンなど低遅延が必要とされる科学研究、電子機械の検証試作ヘの活用が期待される。

主な仕様

・ 型番　hayate_imu rev.C 6軸フュージョン or ver.B 9軸フュージョン切替可能
・ 内蔵チップ　Cortex-M0+、TDK Invensense ICM-20948(9軸)実装 ※1
・ 外部接続　USB Type-Cコネクタ、USB +5V給電 ※2 ※3
・ 最大出力レート ※4
　　-　6軸フュージョン or 9軸フュージョン回転ベクトル四元数　225Hz
　　-　加速度(アクセル)3軸センサ　　225Hz
　　-　角速度(ジャイロ)3軸センサ　　225Hz
　　-　地磁気(コンパス)3軸センサ　　70Hz

・ 測定レンジ
　　-　加速度(アクセル)センサ　　±16g
　　-　角速度(ジャイロ)センサ　　±2000dps
　　-　地磁気(コンパス)センサ　　±4900µT

・ 消費電力　50mW以下(環境温度21℃の実測値)
・ 寸法　30mm × 31.4mm × 4.8mm(突起物含む)
・ 重量　4g以下
・ 取付穴　M3x4、隣り合う穴の中心間距離24.4mm

※1 内蔵Cortex-M0+とICM-20948間インターフェースはSPI(4Mbps)使用、加速度センサ(消耗)、角速度センサ(温度、ドリフト)、地磁気センサ(磁気変動)にダイナミック補正。
※2 USB対向装置OS環境 Ubuntu 16.04以降推奨。
※3 USB対向装置ROS環境 Kinetic以降推奨。
※4 最大出力レートはhayate imuの実力値、IMU対向装置(USB接続先)での実効値はその装置のリソース(CPUクロック周波数、メモリ容量・スピード)に関わる。

デモ情報

・hayate_imu ROSパッケージ | Githubリポジトリ

・9軸IMUセンサ ICM-20948内蔵 6軸／9軸シュージョン 出力レート225Hz 低遅延 USB出力 ROS対応 | YouTube

9dof_hayate_imu_youtube
9dof_hayate_imu_youtube

販売情報

【製品名称】hayate_imu rev.C 6軸フュージョン or ver.B 9軸フュージョン
【開発会社】ROBOT翔（株式会社翔雲）
【発売時期】令和3年4月上旬頃
【取扱店舗】9軸IMUセンサ 6軸／9軸フュージョン 低遅延 USB出力 補正済み ROS対応 | ROBOT翔

後継機種

9軸センサーICM-42688+MMC5983 6軸&9軸回転ベクトル&3軸オイラー角 MAX1000Hz同時出力 ROS/ROS2対応 USB接続

参考資料

Migrating from MPU-9250 to ICM-20948-InvenSense
http://wiki.ros.org/ja/9dof_hayate_imu

関連記事

参考情報

エンコーダ付きDCモータPID制御の実験-hayte_imu応用例
9軸IMUセンサ ICM-20948をロボットに組み込もう
オイラー角～ジンバルロック～クォータニオン
ROS・Unity・ロボット・ドローン姿勢制御に関わるクォータニオン

1+

ロボット・ドローン部品お探しなら
ROBOT翔・電子部品ストア

9軸IMUセンサ ICM-20948をロボットに組み込もう

はじめに

TDK Invensense製9軸IMUのICM-20948は、MPU-9250の後継機種で、MPU-9250のVDDは2.4V～3.6V、VDDIOは1.71V～VDDに対して、ICM-20948のVDDは1.71V～3.6V、VDDIOは1.71V～1.95Vに低めに設定して、省電力となった。また、デジタルモーションプロセッサDMP(ICM-20948内蔵FPGA)によるデータフュージョン(FPGAによるFusion)の特長が継承して、さらにRAM容量が拡張して、6軸フュージョンのみならず9軸フュージョンまで増強して、較正機能もあると、以下参考文献を読むと詳細まで分かる。

環境

・Ubuntu 18.04
・ROS Melodic
・MCU: Cortex M0+
・IMU: ICM-20948

DMP3の出力確認

以下のように、出力レート50Hz、加速度Ax Ay Az、角速度Gx Gy Gz、磁場Mx My Mz、4元数Qw Qx Qy Qzの順に出力させる。

imu-icm20948-output
imu-icm20948-output

4時間+にわたる連続動作して出力を確かめる。確認環境は完全に静止な状態でもないので、ドリフトは納得いく範囲内にとどまっている。rvizで確かめてもドリフトが肉眼では見えないほど。ドリフトにおいては、MPU-9250から大いに改善されたと見られる。

imu-icm20948-output-4hours
imu-icm20948-output-4hours

出力確認動画は以下イメージをクリックすると、youtubeへジャンプする。

icm20948_imu_ros
icm20948_imu_ros

最後に

MPUシリーズと比べて、ユーザの事前校正いらず、長時間(実験は4時間程度まで）においても、ドリフトとくにヨウ角（Yaw、方向角）のドリフトは目立たないほどになった。また、1.71Vの低電圧でも動作可能なのでスマートデバイスや、ロボットの長時間電池駆動が可能になる。なお、出力レートはMax 225Hzと確認できた。ICM-20948 DMP3(IMU内蔵FPGA)から出力した、Accel/Gyro/Mag計9軸データ出力にFusion Quaternionの4元数データがそのまま利用可能で、遅延もソフト・カルマンフィルタなどより少なく他機種IMUより優れる（低遅延、6軸／9軸フュージョンデータ出力レート225Hz）ため、ロボットの精度向上に利用可能。1.8V VDDIO対応、DMP3の出力に手間かかった末、地磁気センサ出力は75Hzまでと少し残念だが、総じて優秀としか思わないICM-20948をロボット装置に組み込もうと決めた。

商品化モジュール

ICM-20948とCoretex M0+を組み込んだ回路を設計して、ROSに対応したロボット専用センサモジュールとして商品化して、2021年1月～、リリースと予定している。この商品は皆さんの学術研究にお役に立てるようと願う。主な仕様は以下のとおり。
・構成　CortexM0+ & TDK Invensense ICM-20948(9軸)実装
・接続　USB Type-Cコネクタ実装
・出力　6軸／9軸融合4元数はFPGA on chipから低遅延で出力、別途ソフトでフュージョン必要なし、出力レート225Hz、同時に加速度(アクセル)3軸データ225Hz、角速度(ジャイロ)3軸データ225Hz、地磁気(コンパス)3軸データ75Hzまで出力可能
・ROSパッケージ、Githubへ公開、ROS Kinetic以降対応、ROS TopicへSubscribeすることでデータが受け取り可能
・rviz実演、実演ビデオあり

【2021年3月いま現在】1回目制作分（評価版）、大学など研究機関へ無料配布中（アンケート調査あり）、WEBでの募集を含めて順次終了。

【2021年4～5月予定】2回目制作分（商用版）、販売の予定。

詳細情報

9軸IMUセンサ 6軸／9軸フュージョン 低遅延 USB出力 補正済み ROS対応

取扱店舗

9軸IMUセンサ 6軸／9軸フュージョン 低遅延 USB出力 ROS対応 | ROBOT翔

参考文献

Migrating from MPU-9250 to ICM-20948-InvenSense

関連記事

9軸IMUセンサ MPU-9250をロボットに組み込もう
6軸IMUセンサ MPU-6050をロボットに組み込もう

2+

ロボット・ドローン部品お探しなら
ROBOT翔・電子部品ストア

9軸IMUセンサ MPU-9250をロボットに組み込もう

はじめに

9軸IMUのMPU-9250はTDK InvenSense社製I2Cインターフェースの3軸ジャイロセンサ+3軸加速度センサ+3軸コンパスセンサIC、内蔵DMP(Digital Motion Processor)機能を使うことで、補正済みデータとしての4元数Quaternionまたはオイラー角、ロールRoll・ピッチPitch・ヨウYaw角の出力が選べる。また、MPUシリーズはすでに新規設計非推奨になっているため、後継機種はICMシリーズで、MPU-9250の後継機種はICM-20948となって、MPU-9250に比べて、事前校正不要で、ドリフトの低減、省電力などにおいてパフォーマンスが改善された。本文は、6軸MPU-6050に続いて、9軸MPU-9250 DMPから4元数Quaternionを読み込んで可視化するまでの手順を以下のとおりに示して、ROSドライバをGithubへ公開する。安価のため、MPU-9250サンプルの入手ルートはAliexpressにした。

mpu6050-mpu9250
mpu6050(6軸)-mpu9250(9軸)

※I2Cインターフェースは、vcc、gnd、scl、sdaの4pinインターフェース

環境

・ubuntu 18.04 Tinker board(or Raspiberry Pi, PC)
・ROS melodic
・DFRobot Romeo mini v1.1(or arduino uno互換)
・MPU-9250/6500

準備①

・ros-melodic-rosserial-arduino、ros-melodic-rosserial、rviz_imu_pluginを入れる

$sudo apt-get update
$sudo apt-get install ros-melodic-rosserial-arduino
$sudo apt-get install ros-melodic-rosserial
$cd ~catkin_ws/src/
$git clone -b melodic https://github.com/ccny-ros-pkg/imu_tools
$cd ..
$catkin_make_isolated

・mpu9250_imu_rosを入れる

$cd ~/catkin_ws/src/
$git clone https://github.com/soarbear/mpu9250_imu_ros.git
$cd ~/catkin_ws/
$catkin_make_isolated

準備②

・firmware/MPU9250_DMP/MPU9250_DMP.inoをArduino IDEでArduinoに書き込む。

imu/dataの可視化

・実に使われるポートtty????を確認する。
・rvizが自動起動して、画面にあるセンサの動きを観察する。

$sudo ls -l /dev/ttyACM*
$sudo chmod 777 /dev/ttyACM0
$roslaunch mpu9250_imu_driver mpu9250_imu.launch

・以下スクリーンショットをクリックすると、youtubeへ遷移する。

mpu6050_imu_ros
mpu9250_imu_ros

センサ融合について

MPU-9250内蔵DMPおよび、センサ融合またはデータ同化Fusionに定番アルゴリズムであるKalman Filterの他、Complementary Filter、Madgwick Filterがある。振動やシステム誤差によって測定値に大きな影響あり、フィルタリングが必須とは言える。

ソースコード

mpu9250_imu_rosソースコード(Github)

後継機種

ICM-20948はMPU-9250の後継機種、その製品化情報は 9軸IMU/AHRS 6軸&9軸回転ベクトル&3軸オイラー角 MAX1000Hz同時出力 ROS/ROS2対応 USB接続、9軸IMU 6軸／9軸フュージョン ICM-20948 Cortex-M0+内蔵 ROS対応

参考文献

1-Jeff Rowberg氏: I2C driver
2-ROS Repository: ROS imu_tools

関連記事

9軸IMU/AHRS 6軸&9軸回転ベクトル&3軸オイラー角 MAX1000Hz同時出力 ROS/ROS2対応 USB接続
9軸IMUセンサ 6軸／9軸フュージョン 低遅延 USB出力 補正済み ROS対応
9軸IMU ICM-20948をロボットに組み込もう
6軸IMU MPU-6050をロボットに組み込もう

3+

ロボット・ドローン部品お探しなら
ROBOT翔・電子部品ストア

6軸IMUセンサ MPU-6050をロボットに組み込もう

はじめに

6軸IMUのMPU-6050はTDK InvenSense社製I2Cインターフェースの3軸ジャイロセンサ+3軸加速度センサIC、amazonで格安販売されている。内蔵DMP(Digital Motion Processor)機能を使うことで、補正済みデータとしての4元数Quaternionまたはオイラー角、ロールRoll・ピッチPitch・ヨウYaw角の出力が選べる。本文は6軸MPU-6050 DMPから、4元数Quaternionを読み込んで可視化するまでの手順を以下のとおり示して、ROSドライバをGithubへ公開する。また、MPU-6050を本文のArduinoに接続ではなくMain BoardのI2Cポートへ繋ぐなどの方法がある。また、MPUシリーズはすでに新規設計非推奨になっているため、ICMシリーズは後継機種となっている。安価のため、MPU-6050サンプルの入手ルートはAliexpressにした。

mpu6050-mpu9250
mpu6050(6軸)-mpu9250(9軸)

※I2Cインターフェースは、vcc、gnd、scl、sdaの4pinインターフェース

環境

・ubuntu 16.04 Tinker board(or Raspiberry Pi, PC)
・ROS kinetic
・DFRobot Romeo mini v1.1(or arduino uno互換)
・MPU-6050 GY-521

準備①

・ros-kinetic-rosserial-arduino、ros-kinetic-rosserial、rviz_imu_pluginを入れる

$sudo apt-get update
$sudo apt-get install ros-kinetic-rosserial-arduino
$sudo apt-get install ros-kinetic-serial
$cd ~catkin_ws/src/
$git clone -b kinetic https://github.com/ccny-ros-pkg/imu_tools
$cd ..
$catkin_make --pkg imu_tools

・mpu6050_imu_rosを入れる

$cd ~/catkin_ws/src/
$git clone https://github.com/soarbear/mpu6050_imu_ros.git
$cd ~/catkin_ws/
$catkin_make

準備②

・mpu6050_imu_driver/firmware/MPU6050_DMP6/MPU6050_DMP6.inoをArduino IDEでArduinoに書き込む。

imu/dataの可視化

・実に使われるポートtty????を確認する。
・rvizが自動起動して、画面にあるセンサの動きを観察する。

$sudo ls -l /dev/ttyACM*
$sudo chmod 777 /dev/ttyACM0
$roslaunch mpu6050_imu_driver mpu6050_imu.launch

・以下スクリーンショットをクリックすると、youtubeへ遷移する。

mpu6050_imu_ros
mpu6050_imu_ros

センサ融合について

MPU-6050内蔵DMPおよび、センサ融合またはデータ同化Fusionに定番アルゴリズムであるKalman Filterの他、Complementary Filter、Madgwick Filterがある。振動やシステム誤差によって測定値に大きな影響あり、フィルタリングが必須とは言える。

校正

ジャイロのドリフト、加速度センサのバイアスの校正が必要、i2cdevlibのArduino/MPU6050/examples/IMU_Zeroをarduinoに入れてオフセットを読み取り、MPU6050_DMP6.inoに盛り込む。またドリフトに対して、時間平均などキャンセリング手法の取り組みも必要だろう。

感想

「ないよりマシ」の観点から、マイナスにならないが、精度があまり追求しないロボットなどに使用可能と考えられる。ジャイロセンサの温度特性あり、またドリフトは時間とともに蓄積するので、一方加速度センサのバイアスが測定毎にあり、ただし蓄積しないので、最初から校正Calibrationの方法を講じることを考えれば、DMP機能まで用意されて可用性がある。Yaw方位角がジャイロから積分計算して合成していないので要注意で、他のセンサ例えばコンパスまたSlam Lidarなどとの組み合わせが可能である。

ソースコード

mpu6050_imu_rosソースコード(Github)

参考文献

Jeff Rowberg氏：I2C driver
ROS Repository：ROS imu_tools

関連記事

9軸IMU/AHRS 6軸&9軸回転ベクトル&3軸オイラー角 MAX1000Hz同時出力 ROS/ROS2対応 USB接続
9軸IMUセンサ 6軸／9軸フュージョン 低遅延 USB出力 補正済み ROS対応
9軸IMU ICM-20948をロボットに組み込もう
9軸IMU MPU-9250をロボットに組み込もう

2+

ロボット・ドローン部品お探しなら
ROBOT翔・電子部品ストア