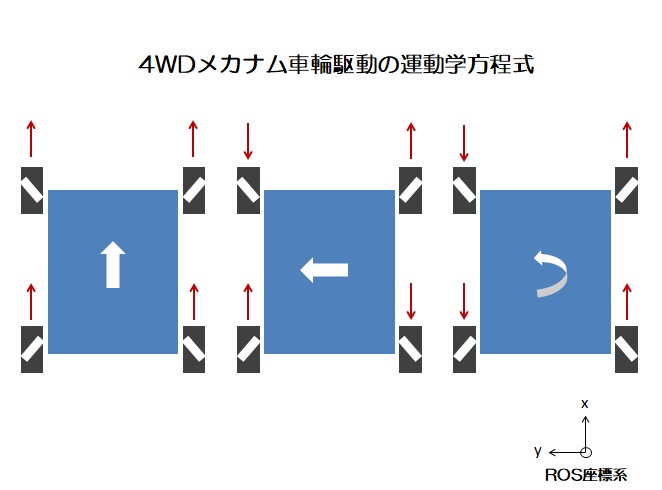
順運動学forward kinematic方程式
メカナム車輪の回転速度はロボット車体中心のx・y軸方向線形速度とz軸まわりの角速度より、以下の式(順運動学方程式)で表される。
// 左右輪距離、前後輪距離 #define WHEEL_SEPARATION_WIDTH DISTANCE_LEFT_TO_RIGHT_WHEEL/2 #define WHEEL_SEPARATION_LENGTH DISTANCE_FRONT_TO_REAR_WHEEL/2 // 回転速度単位:rad / s wheel_front_left =(linear.x-linear.y-(WHEEL_SEPARATION_WIDTH+WHEEL_SEPARATION_LENGTH)*angular.z)/WHEEL_RADIUS; wheel_front_right=(linear.x+linear.y+(WHEEL_SEPARATION_WIDTH+WHEEL_SEPARATION_LENGTH)*angular.z)/WHEEL_RADIUS; wheel_rear_left =(linear.x+linear.y-(WHEEL_SEPARATION_WIDTH+WHEEL_SEPARATION_LENGTH)*angular.z)/WHEEL_RADIUS; wheel_rear_right =(linear.x-linear.y+(WHEEL_SEPARATION_WIDTH+WHEEL_SEPARATION_LENGTH)*angular.z)/WHEEL_RADIUS; // 右に配置されるたモータの逆転が必要 wheel_front_right=-1*wheel_front_right wheel_rear_right =-1*wheel_rear_right
順運動学方程式の簡単な証明
ロボットがx軸方向へ移動の場合
$$\begin{bmatrix}v_{front-left}\\v_{front-right}\\v_{rear-left}\\v_{rear-right}\end{bmatrix}=\begin{bmatrix}linear.x\\linear.x\\linear.x\\linear.x\end{bmatrix}$$
ロボットがy軸方向へ移動の場合
$$\begin{bmatrix}v_{front-left}\\v_{front-right}\\v_{rear-left}\\v_{rear-right}\end{bmatrix}=\begin{bmatrix}-linear.y\\linear.y\\linear.y\\-linear.y\end{bmatrix}$$
z軸まわりロボット中心をめぐる回転の場合
$$\begin{bmatrix}v_{front-left}\\v_{front-right}\\v_{rear-left}\\v_{rear-right}\\width\\length\end{bmatrix}=\begin{bmatrix}-(width+length)*angular.z/2\\(width+length)*angular.z/2\\-(width+length)*angular.z/2\\(width+length)*angular.z/2\\distance_{left2right}\\distance_{front2rear}\end{bmatrix}$$
以上の式を合わせると、順運動学方程式が導かれる。
逆運動学backward kinematic方程式
ロボット車体中心のx・y軸方向線形速度とz軸まわりの角速度は、メカナム車輪の回転速度より、以下の式(逆運動学方程式)で表される。
linear.x =(wheel_front_left+wheel_front_right+wheel_rear_left+wheel_rear_right)*WHEEL_RADIUS/4; linear.y =(-wheel_front_left+wheel_front_right+wheel_rear_left-wheel_rear_right)*WHEEL_RADIUS/4; angular.z=(-wheel_front_left+wheel_front_right-wheel_rear_left+wheel_rear_right)*WHEEL_RADIUS/(4*(WHEEL_SEPARATION_WIDTH+WHEEL_SEPARATION_LENGTH))
