概要
本文には、大文字表現=行列/マトリクス、\(\boldsymbol{Bold}\)小文字表現=d次元(特徴量)ベクトル\(R^d\)、普通小文字表現=スカラー\(R\) と記す。
ロジスティック回帰(Logistic Regression)は、sigmoid関数を介して線形回帰\((\boldsymbol{w}^T\boldsymbol{x}+b)\)を\(0|1\)にマッピングして2クラス問題に適用される。Nクラス分類問題の場合、\((\boldsymbol{w}^T\boldsymbol{x}+b)\)のNセットを取得してから例えばsoftmax関数で振り分ける多重分類問題に適用される。「回帰」の表現があるのに、実はロジスティック分類である。線形回帰\((\boldsymbol{w}^T\boldsymbol{x}+b)\)を利用したわけではないかと考えられる。
線形回帰の表現
$$ f(\boldsymbol{x}) = \boldsymbol{w}^T\boldsymbol{x} + b $$
ただし、\(\boldsymbol{w},\boldsymbol{x} \in R^d,\space b\in R, \boldsymbol{w}’=[b \space \space \boldsymbol{w}]^T, \boldsymbol{x}’ =[1 \space \space \boldsymbol{x}]^T \)にすると、上式が以下の式に簡略化される。
$$ f(\boldsymbol{x}’) = \boldsymbol{w’}^T \boldsymbol{x}’ → f(\boldsymbol{x}) = \boldsymbol{w}^T x $$
分類方法
Perception(認知)機能を果たす活性化関数がsigmoid関数で\(0|1\)の2クラスに分類する場合、以下の表現がある。
$$ p = \sigma[f(\boldsymbol{x})] = \frac{1}{1+e^{-f(\boldsymbol{x})}} = \frac{1}{1+e^{-\boldsymbol{w}^T\boldsymbol{x}}} $$
ただし、\(f(\boldsymbol{x}) = \boldsymbol{w}^T\boldsymbol{x}, \sigma=\)sigmoid関数、区間(0,1)に入る。
コスト関数
$$ c(\boldsymbol{w}) = ln[\prod_{i=0}^{n-1} p^{1-y_i}(1-p)^{y_i}] $$ただし、\(y_i=0|1,p=\sigma[f(\boldsymbol{x})]\)
上式コスト関数、\((p|(y_i=0|1)\)の総乗を最大にすると、つまり最尤推定法を適用する。最尤推定(=コスト関数の最大値)には、勾配を利用してコスト関数が早く収束するつまり最大値を求める方法で、\( \boldsymbol{w}^*= \underset{\boldsymbol{w}}{\operatorname{arg max}}(c(\boldsymbol{w})) \)を求めて、分類の境界線を決めることになる。
※ 最尤法あるいは最尤推定法とは任意のある観測値に対して確率を最大にする母数の推定値を求めようとする方法。
コスト関数の勾配
複数標本\((\sum^n)\)に対して、上記コスト関数が\(\boldsymbol{w}\)への勾配は以下の式で求める。
$$ \nabla c(\boldsymbol{w}) = \sum_{i=0}^{n-1}(y_i-p_i) \boldsymbol{x}_i $$
sigmoid関数を選んだかいで、勾配が簡潔に表現可能となる。
勾配上昇
$$ \boldsymbol{w}^*= \underset{\boldsymbol{w}}{\operatorname{arg max}}[c(\boldsymbol{w})] → \boldsymbol{w}_{t}=\boldsymbol{w}_{t-1}+\alpha \nabla c(\boldsymbol{w_{t-1}}) $$
ただし、\(\alpha\)は小さい常数、例えば0.01~0.001にする。指定した回数または\(\boldsymbol{w}\)の変化しなくなるまで\(\boldsymbol{w}\)の更新を繰り返す。\(\boldsymbol{w}\)が\(c(\boldsymbol{w})\)の勾配方向へ繰り返すので\(c(\boldsymbol{w})\)が素早く最大に達する。最後の\(\boldsymbol{w}=\boldsymbol{w}^*\)と見なして、つまりロジスティック回帰の分類器ができてしまう。
ランダム勾配上昇
上記勾配上昇をさらに工夫して、\(\nabla c(\boldsymbol{w})\)をランダム関数\(g(\boldsymbol{w})\)に置き換えると速くコスト関数cの最大値に辿り着く場合がある。勿論、この置き換え関数の期待値がを勾配に等しいのを満たす必要があり、勾配値の周りにランダムな変動に相当する。
$$ \boldsymbol{w}_{t}=\boldsymbol{w}_{t-1}+\alpha g(\boldsymbol{w_{t-1}}) $$
分類実施
\(\boldsymbol{w}\)を分かると、前述分類方法で、\(\boldsymbol{x}\)を分類する。
$$ p = \sigma[f(\boldsymbol{x})] \ge 0.5 → Class 1, \space A ,\space etc \\
p = \sigma[f(\boldsymbol{x})] < 0.5 → Class 0,\space B ,\space etc $$
実装の例
クラス\(=2\)、特徴量\(=2\)、標本数\(=m+n\)の標本組、ポイントグループ\(\small A([m,2]|y_i=1)=[(x1_0,x2_0),(x1_1,x2_1),…,(x1_m,x2_m)]\)と、ポイントグループ\(\small B([n-m,2]|y_i=0)=[(x1_{m+1},x2_{m+1)}),…,(x1_n,x2_n)]\)の分類に使わられる境界線\(y=\boldsymbol{w}^T\boldsymbol{x}\)の係数を求めて、境界線を描く。ただし、\(\small \boldsymbol{w},\boldsymbol{x}\in R^d, y\in \{0,1\},\)\(\small \boldsymbol{w}=[b \space \space w1 \space \space w2]^T, \boldsymbol{x}=[1 \space \space x1 \space \space x2]^T\)
ソースコードhttps://github.com/soarbear/Machine_Learning/tree/master/logistic_regression
結果
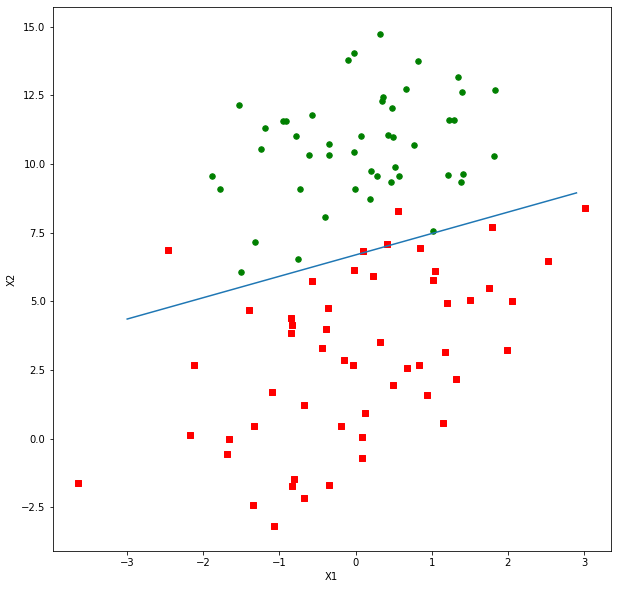
標本の増減により、境界線を計算しなおすのと、正確さから、SVMなどもっと進化した方法論がある。
参考文献
「Machine Learning in Action」、Peter Harrington氏
