概要
本文には、大文字表現=行列/マトリクス、\(\boldsymbol{bold}\)小文字表現=ベクトル\(R^d\)、普通小文字表現=スカラー\(R\) と記す。
複数の弱い分類器を使用して強力な分類器が作れるか。この質問からAdaBoost(Adaptive Boosting)が生まれた。そのプロセスは次のようになる。
訓練用の標本に重み\(\boldsymbol{d}\)を与える。それらの重み\(\boldsymbol{d}\)は等しい値に初期化する。最初に訓練データで弱分類器を訓練して、分類器のエラー率\(\varepsilon\)を計算してから、同じデータセットで訓練を繰り返す。分類器の2回目の訓練では、標本の重み\(\boldsymbol{d}\)が再調整する。そのうち正しく分類された標本の重み\(\boldsymbol{d}\)を減らして、逆に誤分類標本の重み\(\boldsymbol{d}\)を増やす。AdaBoostは複数の弱分類器からそれぞれの分類結果を、それぞれのエラー率に基づいて割り当てられた重み\(\alpha\)で、線形合成して最終の結果にする。分類器のエラー率\(\varepsilon\)と重み\(\alpha\)、標本の重み\(\boldsymbol{d}\)は以下のようになる。
$$ \varepsilon = \frac{\sum misclassified \space samples}{\sum samples} \\ \alpha = \frac{1}{2}ln[\frac{1-\varepsilon}{\varepsilon}] $$ 正しい分類の場合、\( \boldsymbol{d}_i^{t+1} = \frac{\boldsymbol{d}_i^t e^{-\alpha}}{\sum_{i=1}^{n}\boldsymbol{d}} \)
誤分類の場合、\( \boldsymbol{d}_i^{t+1} = \frac{\boldsymbol{d}_i^t e^{\alpha}}{\sum_{i=1}^{n}\boldsymbol{d}} \)
見る瞬間すぐ納得いくようなアルゴリズムなので、実装して結果を確かめよう。
実装の例
AdaBoostの原理で以下5ポイントに対して弱分類器を作って、新たな2ポイントを分類する。
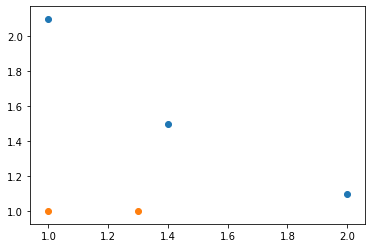
ソースコードhttps://github.com/soarbear/Machine_Learning/tree/master/adaboost
結果

AdaBoostの誤分類がなくなるまで訓練を繰り返すのと複数弱分類器の組み合わせて強分類器になるのがAdaBoostのメリットであり開発に生かしていきたい。
参考文献
[1] PeterHarrington. Machine Learning in Action.
