機械学習の８、決定木

はじめに

本文には、大文字表現=行列／マトリクス、\(\boldsymbol{bold}\)小文字表現=ベクトル\(R^d\)、普通小文字表現=スカラー\(R\) と記す。

決定木は回帰問題に関するアルゴリズムを実現する。決定木には回帰木(Regression Tree)とモデル木(Model Tree)が含まれる。過学習を防ぐために事前剪定(Pre-Pruning)と、決定木の構築後の剪定即ち事後剪定(Post-Pruning)が導入される。最後に、回帰木と標準線形回帰を比較する。

決定木のデータ分割用の特徴量を選択する一般的な方法としてはID3、C4.5、C5.0、CARTアルゴリズムがある。この記事では、主にCARTアルゴリズムを使用する。

CART

CART(Classification And Regression Tree)は決定木アルゴリズムで、２分再帰分割の手法である。分割方法は最小距離ベースのGini係数推定関数を使用して、現在のデータセットを2つのサブセットに分割して2つのサブ木ができてしまう。よってCARTアルゴリズムによって生成される決定木は単純な２分木である。目的変数がカテゴリ変数のときは回帰木(Regression Tree)だが、目的変数が連続数値変数ならモデル木(Model Tree)が得られる。

分割用特徴量と最適な分割点

決定木を使用して回帰問題を解くには、サブ木を生成する分割点としてある特徴量およびその特徴量の値を選択する必要がある。選択基準は分割されたデータの2つの部分に最高の純度を持たせる。離散データの場合、分割されたデータの2つの部分にGini不純物の変化が所定値以下の際の特徴量と分割点を決める。連続変数の場合、データの分散を最小化する最小２乗残差を計算して得られた特徴量と分割点を決める。直感的に理解は分割されたデータの2つの部分に最も近い値を持たせるという。これで以下分割終了条件を満たすまでにデータを分割する。

分割終了条件

・ノード内すべての目的変数の値は同じで、さらに分割する必要はなくこの値を返す。
・木の深さが事前に指定値に達した。
・不純度は指定値よりも小さい、つまりさらに分割必要ない。
・ノード内のデータ量が指定値より少ない。

実装

・5箇所に集まる離散ポイントの回帰木を作成する。
・線状、連続するように見えるポイントのモデル木を作成する。
・モデル木を作成して線形回帰の結果を比較する。
ソースコード
https://github.com/soarbear/Machine_Learning/tree/master/decision_tree

結果

回帰木

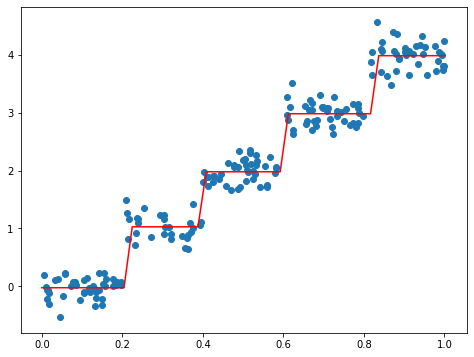
ノード・葉っぱ

regression_tree: {'feat_idx': 0, 'feat_val': 0.400158, 'left': {'feat_idx': 0, 'feat_val': 0.208197, 'left': -0.023838155555555553, 'right': 1.0289583666666666}, 'right': {'feat_idx': 0, 'feat_val': 0.609483, 'left': 1.980035071428571, 'right': {'feat_idx': 0, 'feat_val': 0.816742, 'left': 2.9836209534883724, 'right': 3.9871632}}}

モデル木

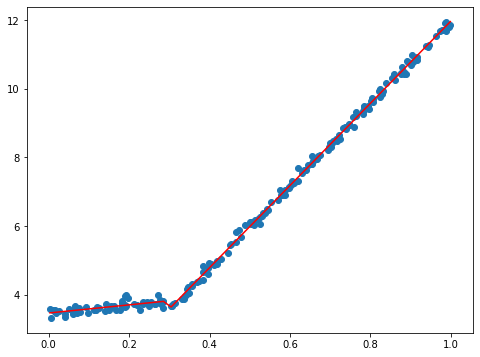
ノード・葉っぱ

mode_tree: {'feat_idx': 0, 'feat_val': 0.304401, 'left': matrix([[3.46877936],
        [1.18521743]]), 'right': matrix([[1.69855694e-03],
        [1.19647739e+01]])}

モデル木と、ノード・葉っぱから見ると、特徴量=0.304401を境目とした２段の直線が分かる。

回帰木と線形回帰の比較

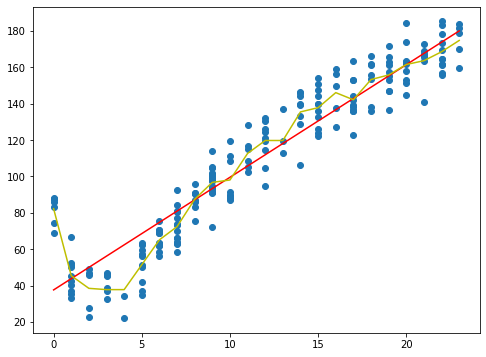
相関係数

linear regression correlation coefficient: 0.9434684235674755
regression tree correlation coefficient: 0.9780307932704089

図、相関係数から見ると線形回帰のほうと比べて回帰木のほうがサンプルポイントに良く相関するのが分かる。

参考文献

[1] PeterHarrington. Machine Learning in Action.