何時もの話っ！

はじめに

本文には、大文字表現=行列／マトリクス、\(\boldsymbol{bold}\)小文字表現=ベクトル\(R^d\)、普通小文字表現=スカラー\(R\) と記す。

決定木は回帰問題に関するアルゴリズムを実現する。決定木には回帰木(Regression Tree)とモデル木(Model Tree)が含まれる。過学習を防ぐために事前剪定(Pre-Pruning)と、決定木の構築後の剪定即ち事後剪定(Post-Pruning)が導入される。最後に、回帰木と標準線形回帰を比較する。

決定木のデータ分割用の特徴量を選択する一般的な方法としてはID3、C4.5、C5.0、CARTアルゴリズムがある。この記事では、主にCARTアルゴリズムを使用する。

CART

CART(Classification And Regression Tree)は決定木アルゴリズムで、２分再帰分割の手法である。分割方法は最小距離ベースのGini係数推定関数を使用して、現在のデータセットを2つのサブセットに分割して2つのサブ木ができてしまう。よってCARTアルゴリズムによって生成される決定木は単純な２分木である。目的変数がカテゴリ変数のときは回帰木(Regression Tree)だが、目的変数が連続数値変数ならモデル木(Model Tree)が得られる。

分割用特徴量と最適な分割点

決定木を使用して回帰問題を解くには、サブ木を生成する分割点としてある特徴量およびその特徴量の値を選択する必要がある。選択基準は分割されたデータの2つの部分に最高の純度を持たせる。離散データの場合、分割されたデータの2つの部分にGini不純物の変化が所定値以下の際の特徴量と分割点を決める。連続変数の場合、データの分散を最小化する最小２乗残差を計算して得られた特徴量と分割点を決める。直感的に理解は分割されたデータの2つの部分に最も近い値を持たせるという。これで以下分割終了条件を満たすまでにデータを分割する。

分割終了条件

・ノード内すべての目的変数の値は同じで、さらに分割する必要はなくこの値を返す。
・木の深さが事前に指定値に達した。
・不純度は指定値よりも小さい、つまりさらに分割必要ない。
・ノード内のデータ量が指定値より少ない。

実装

・5箇所に集まる離散ポイントの回帰木を作成する。
・線状、連続するように見えるポイントのモデル木を作成する。
・モデル木を作成して線形回帰の結果を比較する。
ソースコード
https://github.com/soarbear/Machine_Learning/tree/master/decision_tree

結果

回帰木

ノード・葉っぱ

regression_tree: {'feat_idx': 0, 'feat_val': 0.400158, 'left': {'feat_idx': 0, 'feat_val': 0.208197, 'left': -0.023838155555555553, 'right': 1.0289583666666666}, 'right': {'feat_idx': 0, 'feat_val': 0.609483, 'left': 1.980035071428571, 'right': {'feat_idx': 0, 'feat_val': 0.816742, 'left': 2.9836209534883724, 'right': 3.9871632}}}

モデル木

ノード・葉っぱ

mode_tree: {'feat_idx': 0, 'feat_val': 0.304401, 'left': matrix([[3.46877936],
        [1.18521743]]), 'right': matrix([[1.69855694e-03],
        [1.19647739e+01]])}

モデル木と、ノード・葉っぱから見ると、特徴量=0.304401を境目とした２段の直線が分かる。

回帰木と線形回帰の比較

相関係数

linear regression correlation coefficient: 0.9434684235674755
regression tree correlation coefficient: 0.9780307932704089

図、相関係数から見ると線形回帰のほうと比べて回帰木のほうがサンプルポイントに良く相関するのが分かる。

参考文献

[1] PeterHarrington. Machine Learning in Action.

はじめに

本文には、大文字表現=行列／マトリクス、\(\boldsymbol{bold}\)小文字表現=ベクトル\(R^d\)、普通小文字表現=スカラー\(R\) と記す。

回帰は分類と同じく予測プロセスで、分類との違いは回帰で予測される変数が連続的であるのに対して、分類では離散的だという。回帰は統計学で最も有用なツールである。

線形回帰

線形回帰(Linear Regression)は入力\(X\)に定数\(\boldsymbol{w}\)を乗算して出力\(\boldsymbol{y}\)を得ることができる。これには当てはまらないと他に非線形回帰と呼ばれるのがある。\(\boldsymbol{w}\)の推定値\(\hat{\boldsymbol{w}}\)は最小２乗法(Least Squares Method)から求められて、\(\boldsymbol{w}\)として使われる。
$$ \boldsymbol{y} = X^T\boldsymbol{w} \\ \hat{\boldsymbol{w}} = (X^TX)^{-1}X^T \boldsymbol{y} $$
しかし線形回帰の\(\hat{\boldsymbol{w}}\)は最小２乗の合計から求めた結果で場合により良い結果を予測できなくつまり未学習(Underfitting)となってしまう。以下重み付きで予測誤差を減らそうとする。

重み付き線形回帰

重み付き線形回帰(Locally Weightedlinear RegRession、LWLR)は、より近いポイントが重みをもつようになると予測の正確さが高まる。\(\hat{\boldsymbol{w}}\)は以下のように求める。
$$ \hat{\boldsymbol{w}} = (X^TWX)^{-1}X^TW \boldsymbol{y} $$ガウシアンカーネル関数を用いる場合、 $$ \boldsymbol{w}[i,i] = exp({\frac{|x_i-x|}{-2k^2}}) \\ \boldsymbol{w}[i,j] = 0, \space i \ne j$$
しかし標本数は特徴量より少ない場合、上式の逆行列が求められなく差分を補足してリッジ(Ridge)回帰となる。

リッジ(Ridge)回帰

$$ \hat{\boldsymbol{w}} = (X^TWX+\lambda I)^{-1}X^TW \boldsymbol{y} $$
と同時に、相関している特徴量が存在の可能性あるので、交差検証(Cross Classification)を通して最適の\(\lambda\)を決める。また特徴量を減少(Shrinkage)する方法がある。以下拘束条件を追加するラッソ回帰がある。

ラッソ(Lasso)回帰

$$\sum_{k=1}^n|\boldsymbol{w}_k| \le \lambda $$リッジ(Ridge)回帰、ラッソ(Lasso)回帰より、以下に簡単の方法がある。

前向き段階的回帰

前向き段階的回帰(Forward Stagewise Regression)はラッソ回帰に似てて近い結果が得られる。最初はすべての重みが0に設定されて、各ステップで少しづつ重みの増減を行う。

実装

前向き段階的回帰でポイントグループの回帰係数を求めてみよう。
ソースコード
https://github.com/soarbear/Machine_Learning/tree/master/regression

結果

[[0.    0.    0.    0.001 0.    0.    0.    0.   ]]
[[0.    0.    0.    0.002 0.    0.    0.    0.   ]]
[[0.    0.    0.    0.003 0.    0.    0.    0.   ]]
...
[[ 0.044 -0.011  0.12   0.022  2.023 -0.963 -0.105  0.187]]
[[ 0.043 -0.011  0.12   0.022  2.023 -0.963 -0.105  0.187]]
[[ 0.044 -0.011  0.12   0.022  2.023 -0.963 -0.105  0.187]]

参考文献

[1] PeterHarrington. Machine Learning in Action.

概要

本文には、大文字表現=行列／マトリクス、\(\boldsymbol{bold}\)小文字表現=ベクトル\(R^d\)、普通小文字表現=スカラー\(R\) と記す。

複数の弱い分類器を使用して強力な分類器が作れるか。この質問からAdaBoost(Adaptive Boosting)が生まれた。そのプロセスは次のようになる。

訓練用の標本に重み\(\boldsymbol{d}\)を与える。それらの重み\(\boldsymbol{d}\)は等しい値に初期化する。最初に訓練データで弱分類器を訓練して、分類器のエラー率\(\varepsilon\)を計算してから、同じデータセットで訓練を繰り返す。分類器の2回目の訓練では、標本の重み\(\boldsymbol{d}\)が再調整する。そのうち正しく分類された標本の重み\(\boldsymbol{d}\)を減らして、逆に誤分類標本の重み\(\boldsymbol{d}\)を増やす。AdaBoostは複数の弱分類器からそれぞれの分類結果を、それぞれのエラー率に基づいて割り当てられた重み\(\alpha\)で、線形合成して最終の結果にする。分類器のエラー率\(\varepsilon\)と重み\(\alpha\)、標本の重み\(\boldsymbol{d}\)は以下のようになる。
$$ \varepsilon = \frac{\sum misclassified \space samples}{\sum samples} \\ \alpha = \frac{1}{2}ln[\frac{1-\varepsilon}{\varepsilon}] $$ 正しい分類の場合、\( \boldsymbol{d}_i^{t+1} = \frac{\boldsymbol{d}_i^t e^{-\alpha}}{\sum_{i=1}^{n}\boldsymbol{d}} \)
誤分類の場合、\( \boldsymbol{d}_i^{t+1} = \frac{\boldsymbol{d}_i^t e^{\alpha}}{\sum_{i=1}^{n}\boldsymbol{d}} \)

見る瞬間すぐ納得いくようなアルゴリズムなので、実装して結果を確かめよう。

実装の例

AdaBoostの原理で以下5ポイントに対して弱分類器を作って、新たな2ポイントを分類する。

ソースコードhttps://github.com/soarbear/Machine_Learning/tree/master/adaboost

結果

AdaBoostの誤分類がなくなるまで訓練を繰り返すのと複数弱分類器の組み合わせて強分類器になるのがAdaBoostのメリットであり開発に生かしていきたい。

参考文献

[1] PeterHarrington. Machine Learning in Action.

概要

本文には、大文字表現=行列／マトリクス、\(\boldsymbol{Bold}\)小文字表現=ベクトル\(R^d\)、普通小文字表現=スカラー\(R\) と記す。

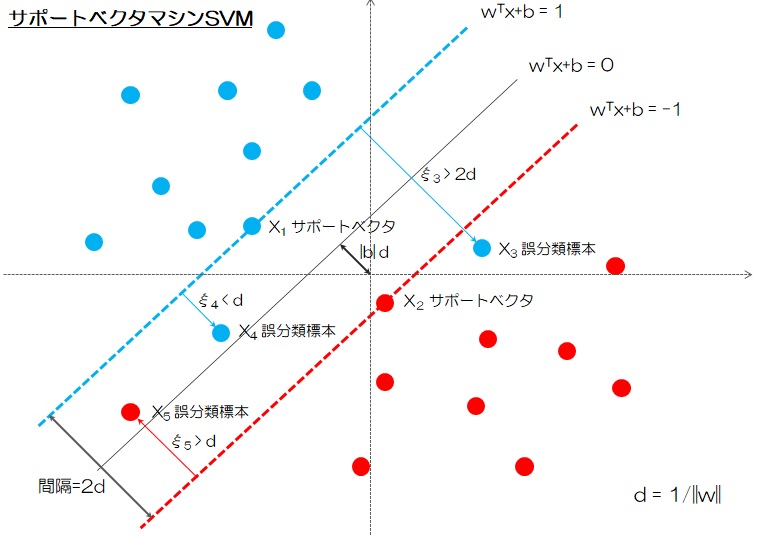
複数の標本(Sample)が分類可能と仮定する場合、直線で異なるラベルに属する標本を分類して、線形SVMが適用される。しかし、このような直線が存在しない場合、カーネルトリック(Kernel Trick)を使用して、写像された高次元空間で標本分類用の超平面(Hyper Plain)が見つかり、非線形SVMが適用される。ロジスティック回帰とは違って、境界(Border)に最も近い標本(Support Vector)の間隔(Margin)を最大化するから、標本が境界にあることが拘束条件(s.t.)である。ラグランジュ乗数法(Lagrange’s method)を利用して拘束条件つきの最適問題を拘束なし問題に簡略化して解くことになる。これで機械学習が一気に難易度を増すことになる。

線形SVM基本形

$$ \underset{w,b}{\operatorname{min}} \frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}\\
s.t. \space \space y_i(\boldsymbol{w}^T \boldsymbol{x_i}+b) \ge 1, \space i=1,2,…,n $$
基本(Primal)形を解くのが難しいから、双対(Dual)形で解くようになる。

線形SVM双対形

$$ \underset{\alpha}{\operatorname{min}} \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j \boldsymbol{x}_i^T \boldsymbol{x}_j -\sum_{i=1}^{n} \alpha_i \\
s.t. \space \space \sum_{i=1}^{n} \alpha_i y_i =0 , \alpha_i \ge 0, i=1,2,…,n $$

線形SVM双対形でも分類できない場合、標本\(\boldsymbol{x}\) を \(\phi(\boldsymbol{x})\)で高次元空間\(R^{\bar{d}}\)に写像する。

非線形SVM基本形

線形SVM基本形から、\(\boldsymbol{x}\)を\( \phi(\boldsymbol{x}) \)に置き換えて以下の式になる。
$$ \underset{w,b}{\operatorname{min}} \frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}\\
s.t. \space \space y_i(\boldsymbol{w}^T \phi (\boldsymbol{x_i})+b) \ge 1, \space i=1,2,…,n $$
カーネル関数は写像(Mapping)された高次元空間における内積(Inner Product)\(\small k(\boldsymbol{x}_i,\boldsymbol{x}_j)= \phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}_j) \)、基本形を解くのが難しいから、双対形で解くようになる。

非線形SVM双対形

非線形SVM基本形から、\(\boldsymbol{x}\)を\( \phi(\boldsymbol{x}) \)に置き換えて以下の式になる。
$$ \underset{\alpha}{\operatorname{min}} \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j \phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}_j) -\sum_{i=1}^{n} \alpha_i \\
s.t. \space \space \sum_{i=1}^{n} \alpha_i y_i =0 , \alpha_i \ge 0, i=1,2,…,n $$

ソフト間隔SVM基本形

理論的にはカーネル関数見つけることができるが、現実においては適切なカーネル関数を見つけることは困難な場合あり、なおかつ標本にはノイズが含まれるから、いかに誤分類なしカーネル関数を求めるなら、オーバーフィッティングに陥てしまう。ここで少量の標本に対して誤分類(Miss-Classification)を許す。
$$ \underset{w,b,\xi}{\operatorname{min}} \frac{1}{2}\boldsymbol{w}^T\boldsymbol{w}+C\sum_{i=1}^{n}\xi_i \\
s.t. \space \space y_i(\boldsymbol{w}^T \phi (\boldsymbol{x_i})+b) \ge 1-\xi_i, \space i=1,2,…,n, \\ \xi_i \ge 0, \space i=1,2,…,n $$
間隔を最適化しながら誤分類が許すが、このような誤分類の標本数がなるべく少なくする必要がある。ここでCが間隔と誤分類の標本数のバランスを取る正則化パラメータで、誤分類をどれだけ許すかを決める。Cが大きくすると誤分類の標本数が少なくなり、Cが小さくすると誤分類の標本数が多くなる傾向がある。\(\xi_i\)はスラック変数(Slackness Variable)と言って、誤分類の度合がどれだけあるのか(どれだけ緩めるか)を表すパラメータである。

ソフト間隔SVM双対形

$$ \underset{\alpha}{\operatorname{min}} \frac{1}{2} \sum_{i=1}^{n} \sum_{j=1}^{n} \alpha_i \alpha_j y_i y_j \phi(\boldsymbol{x}_i)^T \phi(\boldsymbol{x}_j) -\sum_{i=1}^{n} \alpha_i \\
s.t. \space \space \sum_{i=1}^{n} \alpha_i y_i =0 , 0 \le \alpha_i \le C, i=1,2,…,n $$

ヒンジ損失

前述のスラック変数\(\xi\)に関連してヒンジ損失(Hinge Loss)は以下の式で表す。
$$ l(s) = max(0, 1-s) $$ただし、\(s=y_i(\boldsymbol{w}^T \phi (\boldsymbol{x}))\)は標本が正しく分類されるかの信頼度である。標本が正しく分類される場合、ヒンジ損失=0、標本が誤分類される場合、つまり\(s<0\)の場合、ヒンジ損失は大きくなる。まさにヒンジ開閉のように思わせる。

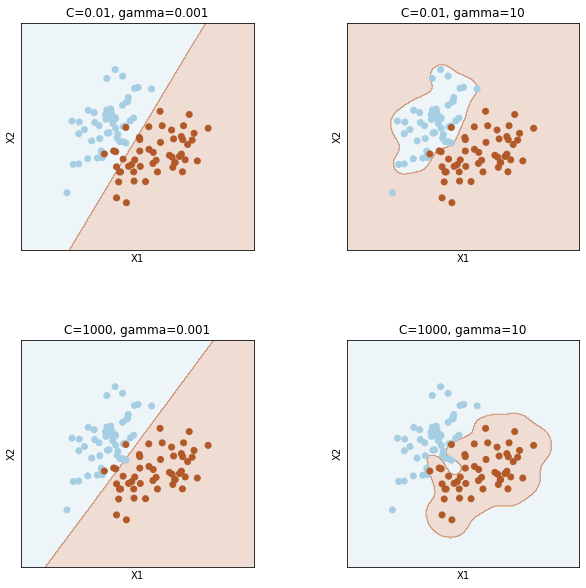
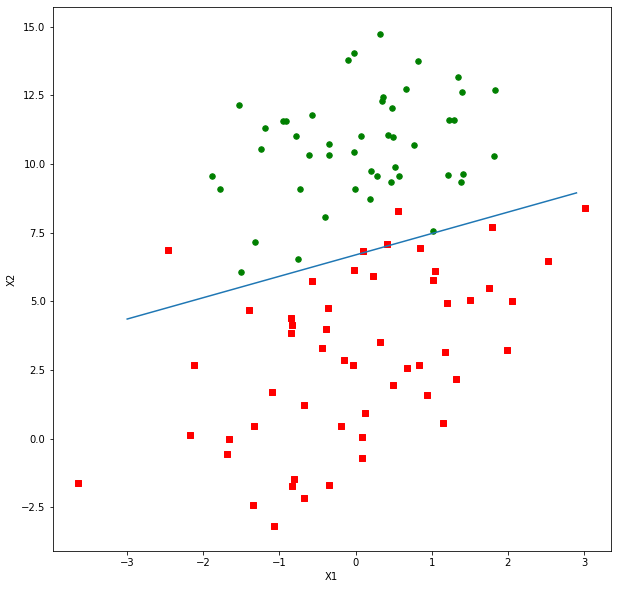
実装の例

pythonのscikit-learnの機能はsklearnというライブラリに組み込まれる。sklearnにsvmというライブラリが内蔵されているので、非常に便利に利用できる。今回は非線形SVMカーネル関数のガウシアンRBF(Gaussian Radial Basis Function)を利用して標本グループを分類してみよう。

\(k(\boldsymbol{x}_i,\boldsymbol{x}_j)= exp(- \gamma (x_i-x_j)^2)\)より、\(\gamma\)はガウシアン曲面の幅を制御する調整用のパラメーターという。特徴量1のガウス分布曲線を思い出すとイメージが分かる。

ソースコードhttps://github.com/soarbear/Machine_Learning/tree/master/svm

結論

サポートベクターマシンSVMのパラメーター\((w,b)\)は、サポートベクターのみに決定されて、他の標本には関係なし。最大間隔により標本数が少なくとも分類の正確さが高い、汎化能力(Generalization Capability)が優れる、非線形問題が解決できるカーネル関数の導入とのメリットをもつ反面、標本数が大きい場合、カーネル関数の内積の計算とラグランジュ乗数の計算に標本数が関連して多大な計算量につながる。標本数は特徴量次元数より遥かに大きい\(n>>d\)場合、深層学習のほうがSVMより優れる。また適切なカーネル関数を選択するのと、ハイパーパラメータを決めるのも難しい。以上の検討結果を開発に取り組んでいきたい。

参考文献

[1] B. E. Boser, I. M. Guyon, and V. N. Vapnik. A training　algorithm for optimal margin classifi ers. In Proceedings of the Annual Workshop on Computational Learning Theory, pages 144–152, 1992.5
[2] S. Boyd and L. Vandenberghe. Convex optimization. Cambridge university press, 2004.4
[3] C.-C. Chang and C.-J. Lin. LIBSVM: A library for support vector machines. ACM Transactions on Intelligent Systems and Technology, 2(3):27, 2011.10
[4] Zhanghao. Derive support vector machine (SVM) from zero. 2018.10

概要

本文には、大文字表現=行列／マトリクス、\(\boldsymbol{Bold}\)小文字表現=d次元(特徴量)ベクトル\(R^d\)、普通小文字表現=スカラー\(R\) と記す。

ロジスティック回帰(Logistic Regression)は、sigmoid関数を介して線形回帰\((\boldsymbol{w}^T\boldsymbol{x}+b)\)を\(0|1\)にマッピングして2クラス問題に適用される。Nクラス分類問題の場合、\((\boldsymbol{w}^T\boldsymbol{x}+b)\)のNセットを取得してから例えばsoftmax関数で振り分ける多重分類問題に適用される。「回帰」の表現があるのに、実はロジスティック分類である。線形回帰\((\boldsymbol{w}^T\boldsymbol{x}+b)\)を利用したわけではないかと考えられる。

線形回帰の表現

$$ f(\boldsymbol{x}) = \boldsymbol{w}^T\boldsymbol{x} + b $$
ただし、\(\boldsymbol{w},\boldsymbol{x} \in R^d,\space b\in R, \boldsymbol{w}’=[b \space \space \boldsymbol{w}]^T, \boldsymbol{x}’ =[1 \space \space \boldsymbol{x}]^T \)にすると、上式が以下の式に簡略化される。
$$ f(\boldsymbol{x}’) = \boldsymbol{w’}^T \boldsymbol{x}’ → f(\boldsymbol{x}) = \boldsymbol{w}^T x　$$

分類方法

Perception(認知)機能を果たす活性化関数がsigmoid関数で\(0|1\)の2クラスに分類する場合、以下の表現がある。
$$ p = \sigma[f(\boldsymbol{x})] = \frac{1}{1+e^{-f(\boldsymbol{x})}} = \frac{1}{1+e^{-\boldsymbol{w}^T\boldsymbol{x}}} $$
ただし、\(f(\boldsymbol{x}) = \boldsymbol{w}^T\boldsymbol{x}, \sigma=\)sigmoid関数、区間(0,1)に入る。

コスト関数

$$ c(\boldsymbol{w}) = ln[\prod_{i=0}^{n-1} p^{1-y_i}(1-p)^{y_i}] $$ただし、\(y_i=0|1,p=\sigma[f(\boldsymbol{x})]\)
上式コスト関数、\((p|(y_i=0|1)\)の総乗を最大にすると、つまり最尤推定法を適用する。最尤推定(=コスト関数の最大値)には、勾配を利用してコスト関数が早く収束するつまり最大値を求める方法で、\( \boldsymbol{w}^*= \underset{\boldsymbol{w}}{\operatorname{arg max}}(c(\boldsymbol{w})) \)を求めて、分類の境界線を決めることになる。

※ 最尤法あるいは最尤推定法とは任意のある観測値に対して確率を最大にする母数の推定値を求めようとする方法。

コスト関数の勾配

複数標本\((\sum^n)\)に対して、上記コスト関数が\(\boldsymbol{w}\)への勾配は以下の式で求める。
$$ \nabla c(\boldsymbol{w}) = \sum_{i=0}^{n-1}(y_i-p_i) \boldsymbol{x}_i $$
sigmoid関数を選んだかいで、勾配が簡潔に表現可能となる。

勾配上昇

$$ \boldsymbol{w}^*= \underset{\boldsymbol{w}}{\operatorname{arg max}}[c(\boldsymbol{w})] → \boldsymbol{w}_{t}=\boldsymbol{w}_{t-1}+\alpha \nabla c(\boldsymbol{w_{t-1}}) $$
ただし、\(\alpha\)は小さい常数、例えば0.01~0.001にする。指定した回数または\(\boldsymbol{w}\)の変化しなくなるまで\(\boldsymbol{w}\)の更新を繰り返す。\(\boldsymbol{w}\)が\(c(\boldsymbol{w})\)の勾配方向へ繰り返すので\(c(\boldsymbol{w})\)が素早く最大に達する。最後の\(\boldsymbol{w}=\boldsymbol{w}^*\)と見なして、つまりロジスティック回帰の分類器ができてしまう。

ランダム勾配上昇

上記勾配上昇をさらに工夫して、\(\nabla c(\boldsymbol{w})\)をランダム関数\(g(\boldsymbol{w})\)に置き換えると速くコスト関数cの最大値に辿り着く場合がある。勿論、この置き換え関数の期待値がを勾配に等しいのを満たす必要があり、勾配値の周りにランダムな変動に相当する。
$$ \boldsymbol{w}_{t}=\boldsymbol{w}_{t-1}+\alpha g(\boldsymbol{w_{t-1}}) $$

分類実施

\(\boldsymbol{w}\)を分かると、前述分類方法で、\(\boldsymbol{x}\)を分類する。
$$ p = \sigma[f(\boldsymbol{x})] \ge 0.5 → Class 1, \space A ,\space etc \\
p = \sigma[f(\boldsymbol{x})] < 0.5 → Class 0,\space B ,\space etc $$

実装の例

クラス\(=2\)、特徴量\(=2\)、標本数\(=m+n\)の標本組、ポイントグループ\(\small A([m,2]|y_i=1)=[(x1_0,x2_0),(x1_1,x2_1),…,(x1_m,x2_m)]\)と、ポイントグループ\(\small B([n-m,2]|y_i=0)=[(x1_{m+1},x2_{m+1)}),…,(x1_n,x2_n)]\)の分類に使わられる境界線\(y=\boldsymbol{w}^T\boldsymbol{x}\)の係数を求めて、境界線を描く。ただし、\(\small \boldsymbol{w},\boldsymbol{x}\in R^d, y\in \{0,1\},\)\(\small \boldsymbol{w}=[b \space \space w1 \space \space w2]^T, \boldsymbol{x}=[1 \space \space x1 \space \space x2]^T\)

ソースコードhttps://github.com/soarbear/Machine_Learning/tree/master/logistic_regression

結果

標本の増減により、境界線を計算しなおすのと、正確さから、SVMなどもっと進化した方法論がある。

参考文献

「Machine Learning in Action」、Peter Harrington氏