タグ: Unity

はじめに

姿勢\(v\)から姿勢\(v’\)への変換はどう表現するのかは、ロボットや、ドローンの開発、運用に避けられない要素である。本文に出ているソースコードは、\(Python\)言語を用いる。

オイラー角、回転行列の表現

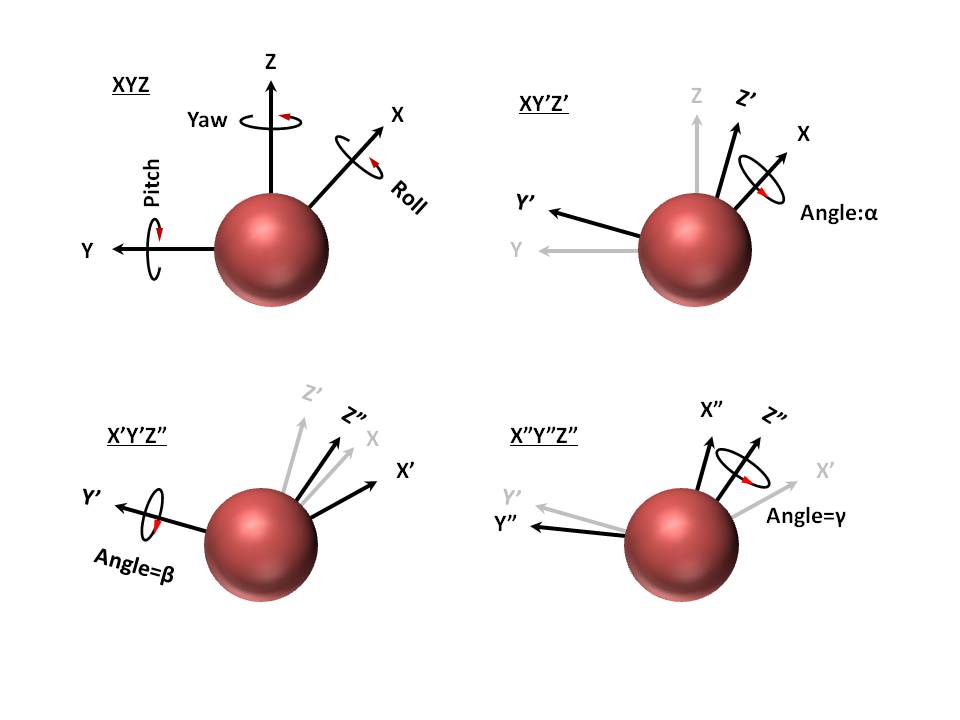
物体を\(X\)軸、\(Y\)軸(\(Y’\)軸)、\(Z\)軸(\(Z”\)軸)まわりの順にそれぞれオイラー角のロール角\(ϕ\)、ピッチ角\(θ\)、ヨー角\(ψ\)だけ回転させたときに、物体の姿勢の変換は、オイラー角と、もしくはオイラー角の三角関数を用いる以下の回転行列で表す。
$$\small R_{xyz} = \begin{bmatrix} CθCψ & -CθSψ & Sθ \\ SϕSθCψ+CϕSψ & -SϕSθSψ+CϕCψ & -SϕCθ \\-CϕSθCψ+SϕSψ & -CϕSθSψ+SϕCψ & CϕCθ \end{bmatrix} $$ ただし、\(C=cos,S=sin\) とする。
しかし、以下のイラストのとおり、オイラー角による姿勢制御の弱点\((Gimbal \space Lock)\)があり、例えば\(Y’\)軸回りを\(90°\)回転すると、\(X’\)軸と\(Z\)軸が同軸となってしまい、以降は姿勢制御(表現)ができなくなる。

このジンバルロックを解消するにはクォータニオンの使命となった。

回転ベクトルの表現

\(ROS\)では回転ベクトルのクォータニオン(四元数)\(q=ix+jy+kz+w\)は、

q=(x,y,z,w)

と表す。原点を通す回転軸を表す単位ベクトル\(a=(ax,ay,az)\)で、この回転軸まわり、角度\(θ\)だけを回転する場合は、クォータニオンは

(x,y,z,w)=(ax*sin(θ/2), ay*sin(θ/2), az*sin(θ/2)，cos(θ/2))

と表す。

以下の例では、\(XY\)平面\((z=0)\)にて辺長\(1m\)の正方形に沿って例えば仮に自律移動ロボットに走行させて、動作を確認しよう。勿論\(Gazebo\)でも確認できる。

\(ROS\)では、ロボットの位置＆姿勢の表現について、ロボットの中心または、ロボットにある他のポイントの位置は\(x,y,z(m)\)、姿勢ポーズはクォータニオンで表す。

from geometry_msgs.msg import Pose, PoseWithCovarianceStamped, Point, Quaternion, Twist  
...
locations['square_vertex_1'] = pose = Pose(Point(1.0,0.0,0.0), Quaternion(0.0,0.0,0.0,1.0))
locations['square_vertex_2'] = pose = Pose(Point(0.0,1.0,0.0), Quaternion(0.0,0.0,0.707,0.707))
locations['square_vertex_3'] = pose = Pose(Point(0.0,1.0,0.0), Quaternion(0.0,0.0,0.707,0.707))
locations['square_vertex_4'] = pose = Pose(Point(0.0,1.0,0.0), Quaternion(0.0,0.0,0.707,0.707))
...

回転ベクトル→オイラー角

geometry_msgs::Quaternion orientation = msg->pose.pose.orientation;    
tf::Matrix3x3 mat(tf::Quaternion(orientation.x, orientation.y, orientation.z, orientation.w));    
double yaw, pitch, roll;    
mat.getEulerYPR(yaw, pitch, roll);

オイラー角→回転ベクトル

tf::Quaternion q;
q.setRPY(Out_X, Out_Y, Out_Z);
sensor_msgs::Imu imu_data;
imu_data.orientation.x=q[0];
imu_data.orientation.y=q[1];
imu_data.orientation.z=q[2];
imu_data.orientation.w=q[3];

関連記事

オイラー角～ジンバルロック～クォータニオン
9軸IMU 6軸／9軸フュージョン 低遅延 USB出力 補正済み ROS対応
研究開発用 台車型ロボット キット