オイラー角
オイラー角とは、3次元ユークリッド空間中の2つの直交座標系(デカルト座標系 )の関係を表現する方法の一つである。ロボット、ドローンの姿勢(ポーズ、向き)を直観に表現するには、オイラー角を用いることがある。オイラー角またはオイラー回転は3つの角度の組に、3座標軸まわりの回転順序(計12通りもある)で表されるので、オイラー角の変数は4つである。ロボットが姿勢\(v\)(ローカル座標系\(XYZ\))から姿勢\(v’\)(ローカル座標系\(X^{\prime \prime}Y^{\prime \prime}Z^{\prime \prime})\)へ変わる際に、例えば\(X\)軸-\(Y’\)軸-\(Z^{\prime \prime}\)軸の順に\(XY’Z^{\prime \prime}\)系オイラー角 \(\alpha,\beta,\gamma\) で3回順次回転することで姿勢の転換を表すことが可能である。【姿勢\(v’\)の座標 = 回転行列・姿勢\(v\)の座標】より、姿勢\(v\)の座標から回転後の姿勢\(v’\)の座標が求められる。姿勢\(v\)の座標、姿勢\(v’\)の座標が分かれば回転行列からオイラー角が求められる場合ある。この場合、積 \( R_{x}( \alpha ) R_{y}( \beta ) R_{z}( \gamma )\) は、\(XY’Z^{\prime \prime}\)回り順で表したときのオイラー角が \( (\alpha,\beta,\gamma) \) であるような回転を表す回転行列\( R_{xyz}(\alpha,\beta,\gamma) \)である。
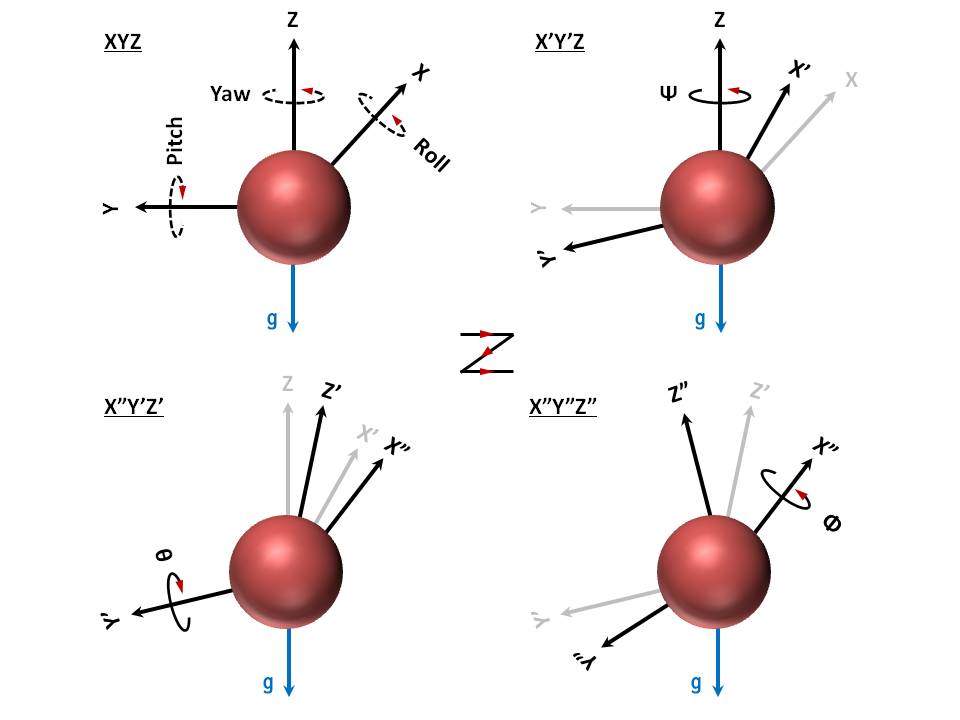
また、回転軸が固定座標軸か機体座標軸により、オイラー角が以下の2種類ほどある。
・固定座標系の3つの軸を中心とした回転、座標軸は静止しているので、固定角という。
・機体座標系の3つの軸を中心とした回転で、回転中に座標軸がロボットとともに回転するため、オイラー角という。
ロボットやドローンが移動の際、固定座標系を参照できないと、姿勢の転換を表すオイラー角を使うしかない場合がある。
ジンバルロック現象、他の問題点
オイラー角の問題点として、オイラー角を使用すると、オイラー角そのものの定義より、ジンバルロック現象を起こしてしまう場合がある。もともとジンバル装置(静態軸ある)で起きる現象で、航空機(剛体)も起きる。但し、固定角にはジンバルロック現象が起きない【※訂正あり】。上記オイラー角の2番目の回転角度\( \beta = ±π/2 \)であれば、1番目回転\( \alpha \)と3番目の回転\( \gamma \)が同じ回転軸になって、つまり\( X \)軸と\( Z^{\prime \prime} \)軸が重なることになる。また回転行列より、\( \alpha – \gamma = C\)にすると、\( \alpha,\gamma \)の解は無限にあることと、1自由度が失われて、3次元空間と2次元空間の違いを考えると、このような3回転はベクトルを平面あるいは錐面に限定されて、すべての3次元ベクトルへ姿勢を変換されず、2自由度にロックされたようにしか考えられぬ現象をジンバルロック現象と呼ばれる。また1ジンバルを1自由度に当てはまると、ジンバルロックといわれるのは分かりやすいだろうか。\( \beta \neq ±π/2 \)であれば、例\( \beta = \pi /3 \)、\( (\alpha , \pi /3 , \gamma) \)の組み合わせであらゆるベクトルに変換可能となる。なお他にジンバルロック現象を起こさないオイラー角\( (\alpha,\beta,\gamma) \)に対して、\( (\alpha+π,π−\beta,\gamma+π) \)の回転で同じ姿勢になる問題点もある。
よって、以下の条件付きであれば、ジンバルロックが除けて、オイラー角でロボットの姿勢を表すのが一意になる。言い換えれば、回転行列がオイラー角と一対一に対応することになる。
・ \( \beta ∈ (-π/2, π/2), \alpha,\gamma ∈ [-π, π] \)
しかし、オイラー角\( (\alpha,\beta,\gamma) \)を制限するのは無理の場合、オイラー角から四元数(Quaternion、クォータニオン)の登場となる。
また、オイラー回転の2番目の回転軸が1番目の回転軸 x 3番目の回転軸の外積の方向にある。つまり、2番目の回転軸が1番目と3番目の回転軸と直交する。当然、1番目と3番目の回転軸が必ずしも直交ではないが、ただし1番目と3番目の回転軸の外積\(=0\)つまり重なるのであれば、ジンバルロックに導く要因となる。
四元数
姿勢あるいは回転の表現には、オイラー角の3回転よりも、単純に回転軸と回転軸まわりの1回転で済む場合、四元数つまり軸回りの回転を表す四元複素数\(( w + ix + jy + kz , w, x, y, z \)は実数、\( i,j,k \)は\(XYZ\)軸に対応する虚数単位\()\)が用いられる。四元数の変数の個数がオイラー角の回転つまり\( [\alpha:Roll,\beta:Pitch,\gamma:Yaw] \)の回転順と同様に4つであり、四元数を見るだけでは姿勢転換のイメージが難しいが、回転軸と回転角の表現に変わると一目瞭然になる。よって、一般論として3次元までの空間の回転の表現に必要な変数の数=空間の次元数+1となる。回転行列からオイラー角を求めるのと、逆に回転順とオイラー角から回転行列を求めるのが面倒だが、四元数を用いて回転を表現すると気持ちがすっきりになる。
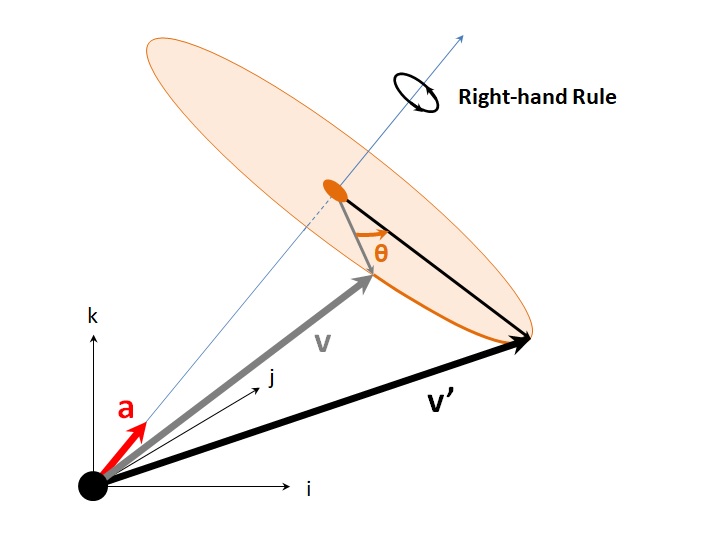
例えば、以下のように、ベクトル\( v=iv_x + jv_y + kv_z\) で表すロボットの姿勢Vを原点を通る単位ベクトル\( a=ia_x + ja_y + ka_z \)を回転軸として、右ねじが進む方向に回転角\(θ\)だけ回転させて、ベクトル\( v’=iv’_x + jv’_y + kv’_z \)で表すロボットの姿勢V’になると、以下に優雅なる表現がある。$$ v’=q v \bar{q} \\ q=cos \frac{θ}{2} + a sin \frac{θ}{2} \\ \bar{q}=cos \frac{θ}{2} – a sin \frac{θ}{2} $$
但し、原点を通る回転軸\(a\)に合わせ、右手の法則に従う回転角\(θ ∈ [-π, π]\)、\(q\)は原点を通る回転軸\(a\)と回転角\(θ\)を組合せた回転ベクトルを表す、正規化した四元数(ノルムは\(1\))、3次元空間における任意の回転に\(q\)は必ず且つ唯一に存在する。\(q,\bar{q}\)は共役または、共軛な複素数、お互いの逆回転でもある。上記計算の結果となる回転後ベクトルの\( v’ \)は回転前ベクトルの\( v\)と同じく、必ず純複素数となって、つまり実数部はゼロになる。
\( ij=-ji=k, jk=-kj=i, ki=-ik=j \)
\( i^2=j^2=k^2=-1, ijk=kk=-1 \)
\( ||a||=1, \space ||q||=||\bar{q}||=1 \)
また、回転 \(q_1\)に引き続き、回転 \(q_2\)を行う場合、次のように書くと良い。
$$ v’=(q_{2}q_{1})v(\bar{q_{1}}\bar{q_{2}}) $$
ロボットの姿勢変換の表現に
\(v=(1,0,0)=i\)をロボットの初期姿勢として、回転軸\(a\)回り、\(\theta\)だけを回転すると、式\(v’=q v \bar{q}\)を使って姿勢変換後の姿勢\(v’\)を求めるように、ロボットの姿勢変換に生かせるようになる。また慣性航法などにも利用されている。なお、四元数はあくまで数なので幾何的にどの表現なのか興味深いが、とにかくひとの脳に想像可能な3次元空間ベクトルに混同しないように注意する。\(q\)はROSで表現すると、\(q.x=(a.x)sin \frac{θ}{2} \\
q.y=(a.y)sin \frac{θ}{2} \\
q.z=(a.z)sin \frac{θ}{2} \\
q.w=cos\frac{θ}{2}\)となる。
簡単な計算例
例:台車ロボットはZ軸回り180°回転してポーズを求めよう。
回転前ポーズ\(v\)を機体前面の法線方向ベクトル\(v=(1,0,0)=i\)に、回転軸\(a=(0,0,1)=k\)、回転角\(\theta=\pi\)として、回転ベクトルは\(q=cos \frac{θ}{2} + a sin \frac{θ}{2} = k\)となる。回転後ポーズは、
\(v’ = q v \bar{q} = (k) (i) (-k) = (k) (k) (i) \\= -i = (-1,0,0)\)と求められる。
検証として、\(z=0\)なので複素平面\(a+bi\)の回転として考えて、\( (1) (i) (i) = (-1, 0, 0) \)と分かる。\(z=0\)を補足すると、四元数の計算結果\((-1,0,0)\)と一致することが分かる。
余談
複素平面\(a+bi\)に実数軸あるのに、なぜ四元数の実数部に対応する座標系の軸はないとか、なぜ三元数は聞いたことはないとかの質問が出るかもしれないが、従来の複素平面\(a+bi\)から拡張された三元数\(a+bi+cj\)はどうも都合は悪くて、使い物にならないので、発明者のHamilton氏(英・数学物理学者)は悩んだすえ、新たに四元数に導いたそうだ。以来、三次元空間における姿勢変換の表現に大いに活用されて、四元数そのものの幾何表現は難問。深くまで掘り下げると、矢野忠先生の「四元数の発見」をご一読ください。
【※訂正】固定角にも、第2回転軸回りの回転角度によって、ジンバルロック現象が起きる。
参考文献
・wiki: オイラー角
・wiki: 四元数
・四元数まとめ資料 – 宇宙電波実験室
関連記事
9軸IMU 6軸/9軸フュージョン 低遅延 USB出力 補正済み ROS対応
ROS・Unity・ロボット・ドローン姿勢の回転表現
SLAM~拡張カルマンフィルタ
SLAM~Unscentedカルマンフィルタ
粒子フィルタ
6軸IMU~拡張カルマンフィルタ
研究開発用 台車型ロボット キット
