概要
株価、為替、天気、動画など時系列データの予測でよく使われるディープラーニングの代表的手法RNN(再帰型ニューラルネットワーク)の拡張バージョンに、LSTM(Long short-term memory)と呼ばれるモデルがある。今回は、LSTM Seq2Seq、Many to Manyモデルを実装して、円の第4象限の一部(訓練未実施)に対して、時系列データの予測を行ってみる。
環境
keras/LSTM, Google Colab CPU
モデル
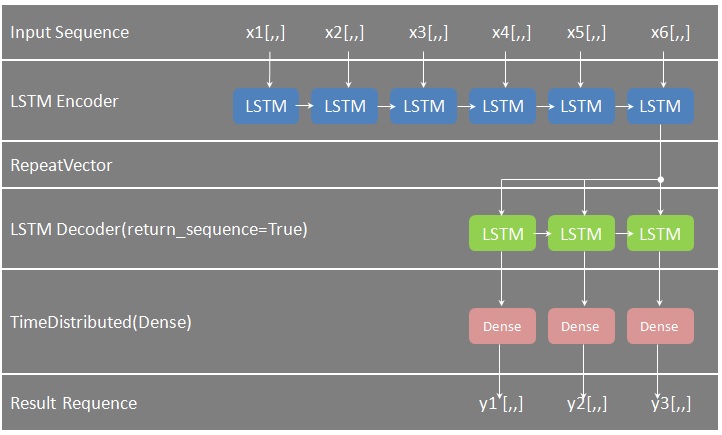
以下モデルの概要を説明する。
・Sequentialは、あるレイヤの全ノードと、次レイヤの全ノードをつなぐRNNのモデル。
・RNNの第1 Layerとして、LSTMを追加する。第1引数は出力の次元数、activationは活性化関数で、input_shapeは入力データのフォーマット(in_time_steps x in_features)となる。このlayerがEncoderのように見える。
・RepeatVectorにより、出力を入力として繰り返す。ここでの繰り返し回数は予測範囲(out_vectors)となる。
・再度のLSTM、ただし、ここではシーケンス出力まさにmany outputつまり、return_sequencesをTrueに指定する。このlayerがDecoderのように見える。
・TimeDistributedを指定し、かつ、Dense(out_features)で、出力の次元数を指定する。
・最後にcompileメソッドで、学習時の最適化手法や、損失関数を指定する。ここでは最適化手法としてAdamを、損失関数としてMSE(Mean Squared Errorつまり平均2乗誤差)に指定する。
実装
# -*- coding: utf-8 -*-
# Brief: A Seq2Seq Model Implementation by keras Recurrent Neural Network LSTM.
# Author: Tateo_YANAGI @soarcloud.com
#
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from keras.models import Sequential
from keras.layers.recurrent import LSTM
from keras.layers.core import Dense, Activation
from keras.layers.wrappers import TimeDistributed
from keras.layers import RepeatVector
PI = 3.1415926535
EPOCHS = 100
TRAIN_SPLIT = 0.98
#
# Class Prediction for lstm model.
#
class Prediction:
def __init__(self):
# Array dimension of input&output:(batch_size, time_steps or vectors, features).
self.batch_size = 48
self.in_time_steps = 6
self.in_features = 2
self.out_vectors = 3
self.out_features = 2
self.hidden_neurons = 100 # Neurons of hidden layer.
self.epochs = EPOCHS # Iteration times.
self.train_split = TRAIN_SPLIT # Partition of learning dataset.
self.activation_hidden = 'tanh' # Activation function for hidden units.
self.activation_output = 'linear' # Activation function for output units.
self.optimizer= 'adam' # Optimization function.
self.loss = 'mse' # Loss(cost) function.
#
# Create dataset.
#
def create_dataset(self, train_split=0.8, in_time_steps=10, out_vectors=4, in_features=2, out_features=2):
a = np.array([[np.cos(0.0), np.sin(0.0)]])
for i in range(1, int(2*PI*10)):
a = np.append(a, np.array([[np.cos(i*0.1), np.sin(i*0.1)]]), axis=0)
print(f'[Debug-0]\nlen(a):{len(a)}\na:\n{a}')
# Create dataset for train and test
# Initialize x_train and y_train.
x_total = a[0:in_time_steps, 0:in_features]
y_total = a[in_time_steps:in_time_steps+out_vectors, 0:in_features]
# Calculate length for x_total and y_total.
total_len = a.shape[0] - in_time_steps - out_vectors + 1
print(f'[Debug-1]\ntotal_len:{total_len}')
# Fill out x_total and y_total.
for i in range(1, total_len):
x_total = np.append(x_total, a[i:i+in_time_steps], axis=0)
y_total = np.append(y_total, a[i+in_time_steps:i+in_time_steps+out_vectors], axis=0)
print(f'[Debug-2]\nx_total.shape[0]):{x_total.shape[0]}\nx_total:\n{x_total}\ny_total.shape[0]:{y_total.shape[0]}\ny_total:\n{y_total}')
# Reshape x_toal and y_total from 2D to 3D.
x_total = np.reshape(x_total[0:x_total.shape[0]], (-1, in_time_steps, in_features))
y_total = np.reshape(y_total[0:y_total.shape[0]], (-1, out_vectors, out_features))
# Split dataset for train and test
x_train = x_total[0:int(x_total.shape[0]*train_split)]
y_train = y_total[0:int(x_total.shape[0]*train_split)]
#x_test = x_total[x_train.shape[0]:]
#y_test = y_total[y_train.shape[0]:]
x_test = x_total[-2:]
y_test = y_total[-2:]
print(f'[Debug-3]\nx_train.shape[0]:{x_train.shape[0]}\nx_train:\n{x_train}\ny_train.shape[0]:{y_train.shape[0]}\ny_train:\n{y_train}')
print(f'[Debug-4]\nx_test.shape[0]:{x_test.shape[0]}\nx_test:\n{x_test}\ny_test.shape[0]:{y_test.shape[0]}\ny_test:\n{y_test}')
return x_train, y_train, x_test, y_test
#
# Create lstm model.
#
def create_model(self) :
model = Sequential()
# Encoder
model.add(LSTM(self.hidden_neurons, activation=self.activation_hidden, input_shape=(self.in_time_steps, self.in_features)))
# Output used as Input.
model.add(RepeatVector(self.out_vectors))
# Decoder, output sequence
model.add(LSTM(self.hidden_neurons, activation=self.activation_hidden, return_sequences=True))
model.add(TimeDistributed(Dense(self.out_features, activation=self.activation_output)))
#model.add(Activation(self.activation_output))
model.compile(optimizer=self.optimizer, loss=self.loss, metrics=['accuracy'])
return model
def train_model(self,model, x_train, y_train) :
model.fit(x_train, y_train, epochs=self.epochs, verbose=2, batch_size=self.batch_size)
return model
#
# main()
#
if __name__ == "__main__":
predict = Prediction()
train_in_data = None
# Create dataset
x_train, y_train, x_test, y_test = predict.create_dataset(predict.train_split, predict.in_time_steps,\
predict.out_vectors, predict.in_features, predict.out_features)
# Create model
model = predict.create_model()
# Train model
model = predict.train_model(model, x_train, y_train)
print(model.summary())
# Test
predicted = model.predict(x_test, verbose=1)
print(f'[info_1]predicted:\n{predicted}')
# Plot result
predicted = np.reshape(predicted, (-1, predict.out_features))
x_test = np.reshape(x_test, (-1, predict.in_features))
y_test = np.reshape(y_test, (-1, predict.out_features))
x_train = np.reshape(x_train, (-1, predict.in_features))
y_train = np.reshape(y_train, (-1, predict.out_features))
plt.figure(figsize=(8, 8))
plt.scatter(x_train[:,0], x_train[:,1])
plt.scatter(x_test[:,0], x_test[:,1])
plt.scatter(y_test[:,0], y_test[:,1])
plt.scatter(predicted[:,0], predicted[:,1])
plt.show()
※ソースコード公開→
https://github.com/soarbear/lstm_seq2seq_model_prediction
結果
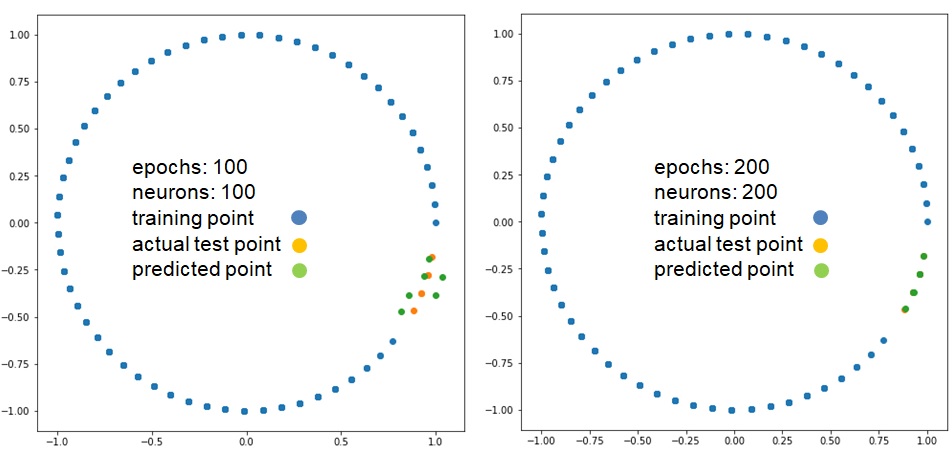
今回、epochsとneuronsを増やすことで、上図のとおり精度において納得いく結果を得た。これでコスト関数、活性化関数の選定はじめ、ハイパーパラメータの調整が精度にいかに重要なことを分かる。熱伝播、振動、柔軟ロボット関節の駆動力など元々フーリエ変換、ラプラス変換、Z変換しか解けない偏微分方程式が、LSTMモデルを適用できたらどうかと今度試してみる。
参考文献
1、LSTMネットワークを理解する(英文原稿)、Christopher Olah氏
2、Keras公式資料
