何時もの話っ！

はじめに

プリズムをかけて赤から紫の順に太陽光のスペクトルを表現させるように、フーリエ級数、フーリエ変換・逆変換、ラプラス変換・逆変換、Z変換・逆変換が、関数の（広義的）周波数特性を解析するとき、必ず登場する。フーリエ変換、ラプラス変換、Z変換の計算式および（広義的）周波数領域におけるイメージ表現の例を以下のように示す。

フーリエ級数

周期2Lの区分的に滑らかな周期関数\(f(t)\)は、不連続点を除いて、$$ f(t) = \frac{1}{2}a_0 + \sum_{n=1}^{\infty} (a_n cos\frac{n\pi}{L}t + b_n sin\frac{n\pi}{L}t) $$ で表される。また実フーリエ級数、フーリエ級数の三角関数表現ともいう。
ただし、\(\small a_0 = \frac{1}{L} \int_{-L}^L f(t)dt , \space a_n = \frac{1}{L} \int_{-L}^L f(t)cos\frac{n\pi}{L}tdt ,\) \( \space b_n = \frac{1}{L} \int_{-L}^L f(t)sin\frac{n\pi}{L}tdt \)

また複素フーリエ級数がフーリエ級数の複素表現ともいう。
$$ f(t) = \sum_{n=1}^{\infty} C_n e^{\frac{in\pi t}{L}} ……①$$ ただし、\(\small C_0 = \frac{1}{2L} \int_{-L}^L f(t)dt,C_n=\frac{1}{2L}\int_{-L}^L f(t)e^{-\frac{in\pi t}{L}}dt ……②\)

周期関数\(f(t)\)が偶関数のとき、フーリエ余弦級数となる。
$$ f(t) = \frac{1}{2}a_0 + \sum_{n=1}^{\infty} a_n cos\frac{n\pi}{L}t $$ただし、\(\small a_0 = \frac{2}{L} \int_{0}^L f(t)dt ,\space a_n = \frac{2}{L} \int_{0}^L f(t)cos\frac{n\pi}{L}tdt \)

周期関数\(f(t)\)が奇関数のとき、フーリエ正弦級数となる。
$$ f(t) = \sum_{n=1}^{\infty} b_n sin\frac{n\pi}{L}t $$ただし、\( b_n = \frac{2}{L} \int_{0}^L f(t)sin\frac{n\pi}{L}tdt \)

フーリエ変換・逆変換

\(f(x)\)が非周期関数のとき、周期2L→無限大にすると、フーリエ級数がフーリエ変換(FT: Fourier Transform)・逆変換(IFT: Inverse Fourier Transform)に拡張される。区分的に滑らかで絶対可積分な関数\(f(x)\)について、式②よりフーリエ変換は次の式で表される。\( F(\omega) \)は式②の\( C_n \)に相当する、いわゆる周波数成分となる振幅である。
$$ F(\omega) = \int_{-\infty}^{\infty} f(x)e^{-i\omega x}dx $$
式①よりフーリエ逆変換は次の式で表される。これで\(F(\omega)\)を元の関数\(f(x)\)に戻す。
$$ f(x) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega)e^{i\omega x}d\omega $$
f(x)が偶関数のとき、フーリエ余弦変換、フーリエ余弦逆変換となる。
$$ F(\omega) = 2\int_{0}^{\infty} f(x)cos\omega xdx \\ f(x) = \frac{1}{2\pi}\int_{-\infty}^{\infty} F(\omega)cos\omega xd\omega $$
f(x)が奇関数のとき、フーリエ正弦変換、フーリエ正弦逆変換となる。
$$ F(\omega) = -2i\int_{0}^{\infty} f(x)sin\omega xdx \\ f(x) = \frac{i}{2\pi}\int_{-\infty}^{\infty} F(\omega)sin\omega xd\omega $$ フーリエ変換の例として、時間領域のデルタ関数（超関数≠普通の関数） \( \delta(x-0) \) の周波数スペクトルは定数 1 になる。つまり周波数に関わらず 1 だから，全部の周波数成分が等しく含まれている。逆にいうと，あらゆる周波数成分を等しく重ね合わせるとデルタ関数が作り出せる（フーリエ逆変換）。

さらに、時刻\( x_1 \) にインパルスが立っているデルタ関数\( \delta(x-x_1) \)はフーリエ変換すると、\( F(\omega) = e^{-i\omega x_1} \) つまり螺旋 \( cos\omega x_1 – isin\omega x_1 \)となる。以上の定数 1 になるのは\(X_1=0\)のときの特例である。

合成積と関数の積

合成積（畳み込み）$$ f*g(t) = \int_{-\infty}^{\infty} f(x)g(t-x)dx $$
合成積のフーリエ変換　$$ F[f*g(t)] = F[f(x)] F[g(x)] $$
関数の積のフーリエ変換 $$ F[f(x)g(x)] = \frac{1}{2\pi} F[f(x)] F[g(x)] $$

フーリエ変換の性質

線形性（重ね合わせの原理） $$ F[af(x)+bg(x)] = aF(\omega)+bG(\omega) $$
伸縮性 $$ F[f(ax)] = \frac{1}{|a|}F(\frac{\omega}{a}) $$
変数シフト $$ F[f(x+a)] = e^{-ia\omega}F(\omega) \\ F[e^{ia\omega} f(x)]=F(\omega-a) $$
対称性 \( F[f(x)]=F(\omega) \)のとき、$$ F[F(x)]=2\pi f(-\omega) $$
共役性 $$ F(-\omega) = \bar{F}(\omega) $$

微分、積分のフーリエ変換

\(f(x)\)が区分的に滑らかで連続、絶対可積分のとき、
$$ F[f'(x)] =i\omega F[f(x)] \\ F[f^{(n)}(x)] = (iw)^{n}F[f(x)] $$
\(f(x)\)が区分的に滑らかで連続、絶対可積分、かつ\( \int_{-\infty}^{\infty}f(x)dx=0 \)の時
$$ F[\int_{-\infty}^{\infty}f(t)dt]=\frac{1}{i\omega}F[f(x)] $$

パーシバルの等式

$$ \int_{-\infty}^{\infty} |f(t)|^2 dt = \frac{1}{2\pi}\int_{-\infty}^{\infty}|F(\omega)|^2 d\omega $$

離散フーリエ変換・逆変換

サンプリング定理から、ある関数（画像、音声など）をそれのもつ最大の周波数の２倍以上の細かさでサンプリングしておけば、つまりサンプリング間隔はナイキスト間隔以下にすれば、サンプリングされたもの（ディジタル画像，ディジタル音声）から元の関数を再現できる。例として、CDはサンプリング周波数が44.1kHz→22.05kHzまでの音声が記録できる。逆にいうと、録音時にそれ以上の周波数の成分が入らないようにしなければならない。またフーリエ逆変換すれば、理論上サンプリング値から得た周波数成分がサンプリング値に戻る。

アナログ信号からサンプリングしたデジタル信号から、フーリエ変換・逆変換は離散フーリエ変換・逆変換と変身する。離散フーリエ変換(DFT: Discrete Fourier Transform)は次の式で表される。
$$ F_n = \frac{1}{N} \sum_{k=0}^{N-1}f_k e^{-i \frac{2n\pi}{N}k} = \frac{1}{N} \sum_{k=0}^{N-1}f_k \bar{\zeta}_{N}^{nk} \\(n=0,1,2,3,…N-1)$$
離散フーリエ逆変換(IDFT: Inverse Discrete Fourier Transform)は次の式で表される。
$$ f_k = \sum_{n=0}^{N-1} F_n e^{i \frac{2n\pi}{N}k} = \sum_{n=0}^{N-1} F_n \zeta_{N}^{nk} \\ (k=0,1,2,3,…N-1)$$
ただし、\( \zeta_{N}^{nk} = e^{i \frac{2n\pi}{N}k}, \space \bar{\zeta}_{N}^{nk} = e^{-i \frac{2n\pi}{N}k}\)

\( \zeta_{N}^{nk} \)をフーリエ行列\( (\zeta_{N}^{nk}) \)にして、フーリエ行列から周波数成分が求まる。フーリエ行列\(M_N\)の複素共役行列による離散フーリエ変換の表現（周波数成分）は次の式で表される。$$ F_N = \frac{1}{N}\bar{M}_Nf_N $$
フーリエ行列\(M_N\)による離散フーリエ逆変換の表現は次の式で表される。$$ f_N = M_NF_N $$ただし、\( M_N = (\zeta_{N}^{nk}), \space \bar{M}_N = (\bar{\zeta}_{N}^{nk}) \)

またフーリエ行列から周波数成分を解く離散フーリエ変換を高速に実行できるのは高速フーリエ変換(FFT: Fast Fourier Transform)である。FFTで計算すると、離散フーリエ変換での\(\small N(2N-1)\)回の計算が、約\( \small \frac{N}{2}(3log_{2}N-1) \)回の計算まで縮まる。\(\small N=2^{10}=1024 \)ならば、2,096,128回の計算が、約14,848回まで減少する。

これで、周波数帯域のスペクトル、ある周波数成分の調べたり、ある周波数成分のフィルタリング（雑音除去）したり、ある周波数成分の挿入したり、フーリエ変換・逆変換が活用される。

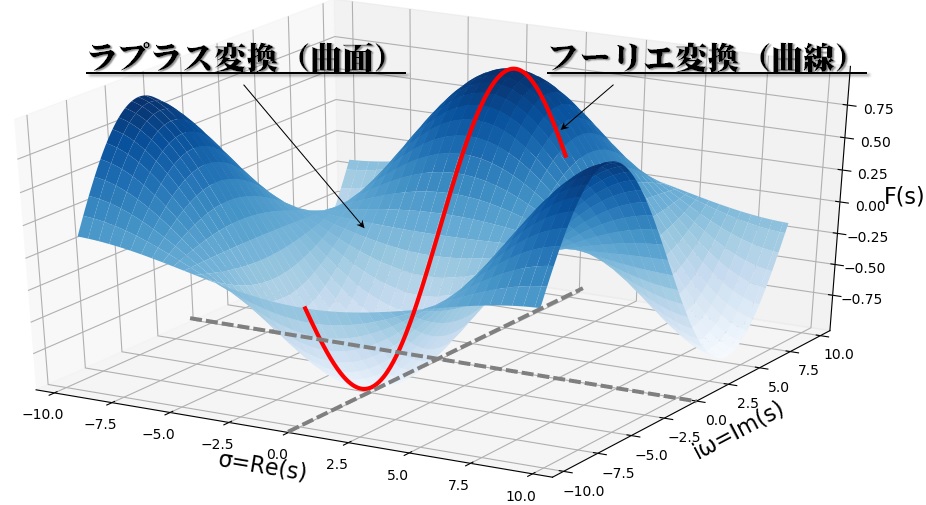
ラプラス変換・逆変換

フーリエ変換の複素数\(i \omega \)から\(s=\sigma+i\omega \)に拡張して、殆どの\(f(t)\)が絶対可積分となって、ラプラス変換は次の式で表される。
$$ F(s) = \int_{-\infty}^{\infty} f(t) e^{-st} dt $$
ラプラス逆変換は次の式で表される。
$$ f(t) = \frac{1}{2\pi i} \int_{\sigma – i\infty}^{\sigma + i\infty} F(s) e^{st} ds $$

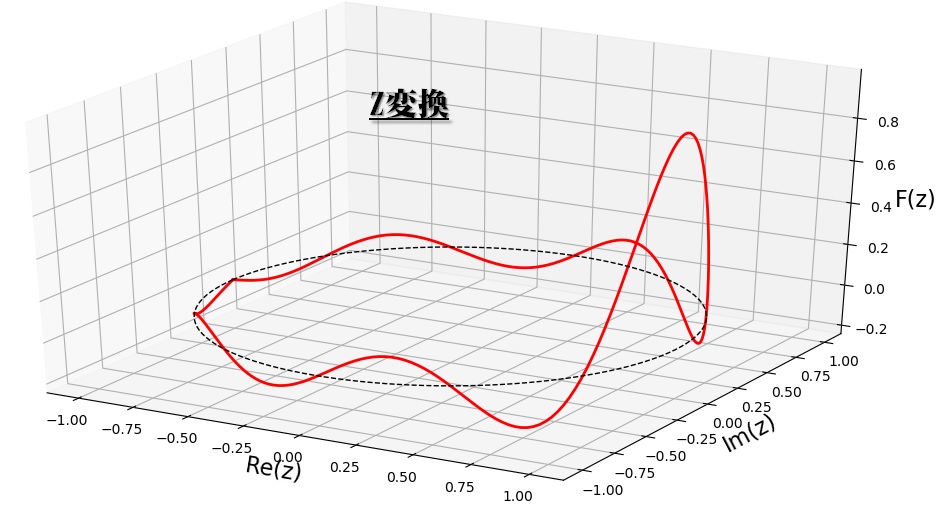
Z変換・逆Z変換

ラプラス変換の\(f(t)\)をサンプリングした離散信号を\( x(n), z = e^{\sigma + i\omega T} \)とおくと、Z変換は次の式で表される。
$$ X(z) = \sum_{n=-\infty}^{\infty} x(n) z^{-n} $$
逆Z変換は次の式で表される。
$$ x(k) = \frac{1}{2\pi i} \oint_{c} X(z) z^{k-1} dz $$

（広義的）周波数領域のイメージ表現例

最後に

共にフランス科学者のフーリエ先生（徒）、ラプラス先生（師）は実の師弟関係だ。減衰振動等微分方程式と代数方程式の橋渡し役、即ち微分方程式の解き方としてのラプラス変換・逆変換が公開されたに対して、波動方程式、熱伝導方程式の解き方として、また完全正規直交関数系である\( \left\{ \frac{1}{\sqrt{2 \pi}},\frac{cos nx}{\sqrt{\pi}},\frac{sin nx}{\sqrt{\pi}} \right\}(n=1,2,3…) \)、つまり実数、正弦関数、余弦関数を組み合わたフーリエ級数から無限次元ベクトル空間が構成可能で、更に条件付き関数を時間領域\(f(t)\)または距離領域\(f(x)\)から周波数領域\( F(\omega)\)の表現に転換可能なフーリエ変換が物事／世界の新たな一面を切り拓いた。やがて離散フーリエ変換に基づいたアナログ～デジタルのサンプリング定理等デジタル信号処理に大いに貢献した。
★Jean Baptiste Joseph Fourier、Baron de、1768年3月21日~1830年5月16日、フランスの数学者・物理学者
★Pierre-Simon Laplace、1749年3月23日~1827年3月5日、フランスの数学者、物理学者、天文学者

参考書籍

フーリエ変換、佐藤敏明氏著、ナツメ社出版
今日から使えるフーリエ変換、三谷政昭氏著、講談社出版