概要 6軸IMU(慣性センサ) =3軸加速度センサ + 3軸ジャイロセンサ に対して拡張カルマンフィルタ をかけてセンサ融合 \((Sensor Fusion)\)またはデータ同化 \((Data Assimilation)\)を行う。\(3\)軸加速度センサにてセンサローカル座標系 (機体座標系と称す)の\(3\)軸における重力加速度g の分量が出力され、観測方程式 によりオイラー角 の\(θ,ϕ\)が計算できる。\(3\)軸ジャイロセンサから機体座標系の\(3\)軸まわりの角速度 が出力され、状態方程式 によりオイラー角 の\(ψ,θ,ϕ\)が計算できる。また、ランダム誤差(ノイズ) が存在し、そしてドリフト が蓄積していくので、拡張カルマンフィルタの状態空間モデル での補正を行う。\(6\)軸\(IMU\)慣性センサまたは\(9\)軸\(IMU\)慣性センサは、ロボット、ドローンなどの位置推定、姿勢推定などに大いに活用されている。本文の固定座標系 は地面から見た、Z軸はUP方向の右手の法則に従う座標系とする。機体座標系 は移動体にあったIMUセンサの座標系で、最初に機体座標系は固定座標系と重なるとする。固定座標系の\(Z, Y, X\)軸回りの固定角 はヨー、ピッチ、ロールとする。本文の姿勢の表現は\(ZY’X^{\prime \prime}\)軸回り順のオイラー角 \(ψ, θ, ϕ\)とする。
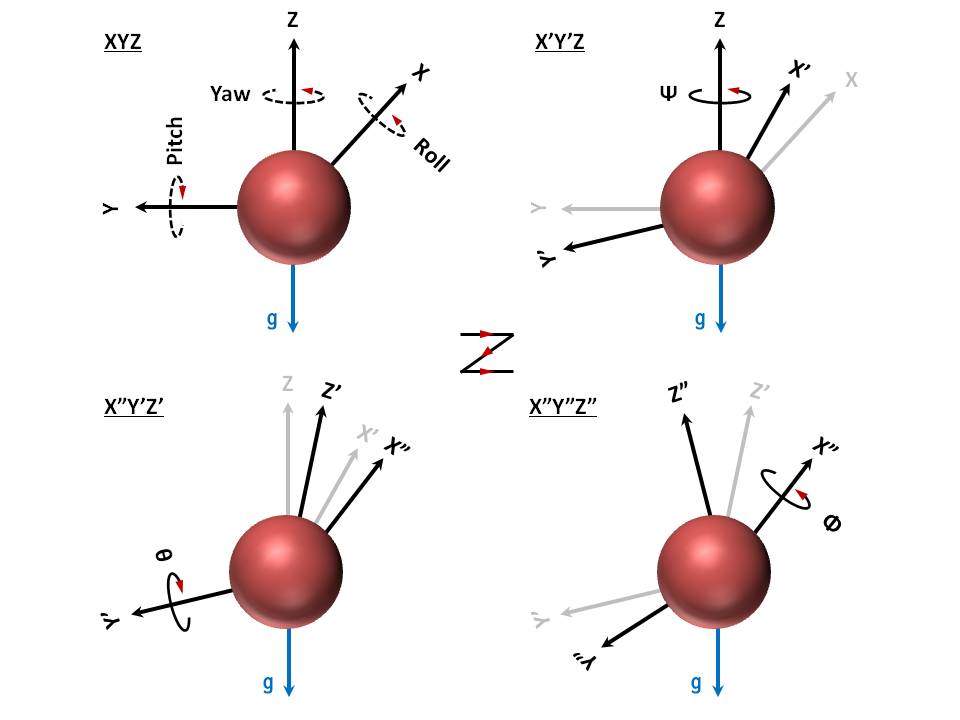
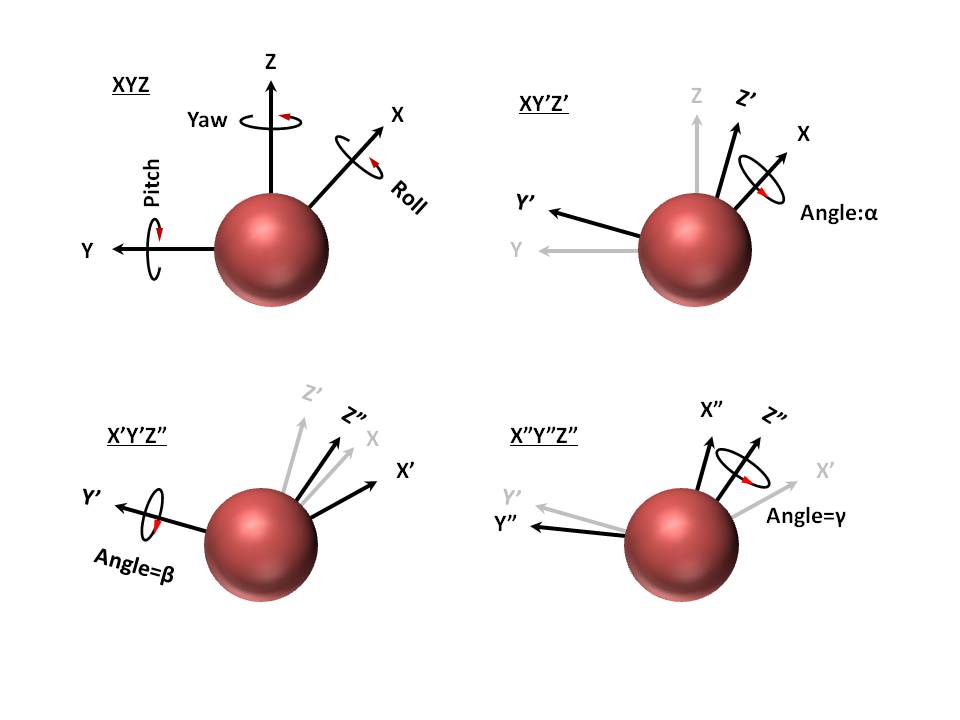
3軸加速度センサ オイラー角 \(ZY’X^{\prime \prime}\)軸回り順として、つまり\(Z\)軸を第\(1\)回転軸、回転角度はオイラー角\(ψ\)、\(Y’\)軸を第\(2\)回転軸、回転角度はオイラー角\(θ\)、\(X^{\prime \prime}\)軸を第\(3\)回転軸、回転角度はオイラー角\(ϕ\)、即ち\(R_z(ψ)→R_y(θ)→R_x(ϕ)\)と記す場合、機体座標系とオイラー角の対応関係は以下の図に示す。オイラー角は必ず軸まわりの回転順と絡むので、変数は\(4\)つと考えても良い。本文では、オイラー角の回転方向と回転軸の関係は右手の法則に従う。固定座標系・機体座標系・オイラー角(右手の法則)
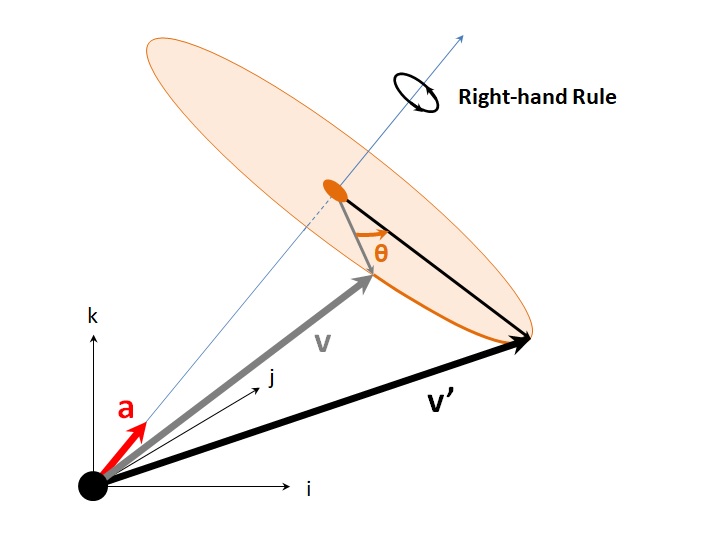
回転行列 固定座標系ベクトル\(p\)は物体座標系とともに、\(Z→Y’→X^{\prime \prime}\)軸まわり順として、それぞれオイラー角 の\(ψ, θ, ϕ\)の回転移動を行って物体座標系ベクトル\(p’\)へ変換された場合、固定座標系ベクトル \(p\)、機体座標系ベクトル \(p’\)、三次元空間回転行列 \(R_{zyx}\)の関係は、以下の式で表現できる。
観測方程式 $$ p’ = \begin{bmatrix} a_x & a_y & a_z \end{bmatrix}^T \\ p = \begin{bmatrix} 0 & 0 &-g \end{bmatrix}^T $$ ただし、\(g\)は重力加速度\( (\simeq 9.81m/s^2 ) \)、\(a_x, a_y, a_z\)は重力加速度が機体座標系\(X^{\prime \prime}Y^{\prime \prime}Z^{\prime \prime}\)軸における成分。
オイラー角\(ϕ,θ\) よって、重力加速度\(g\)の分量により\(3\)軸加速度計センサのオイラー角が以下の式で求める。オイラー角~ジンバルロック~クォータニオン で説明する。
なお、\(ψ\)角は、\(3\)軸加速度センサだけでは推定できないゆえに、\(3\)軸ジャイロセンサまたはコンパスセンサが必要になる。しかし、センサ融合手法として活用された拡張カルマンフィルタは、複数のセンサとも推定できる角度しか求めないので、\(ψ\)角は、以下の拡張カルマンフィルタの状態方程式から除外される。\(ψ\)角の求め方について、角速度\(ω_z\)の時間積分して単独に求められる。または、\(ψ\)角が別途観測可能なコンパスセンサを加え、これで9軸IMU = 6軸IMU + 3軸地磁気センサ で拡張カルマンフィルタが適用するようになる。
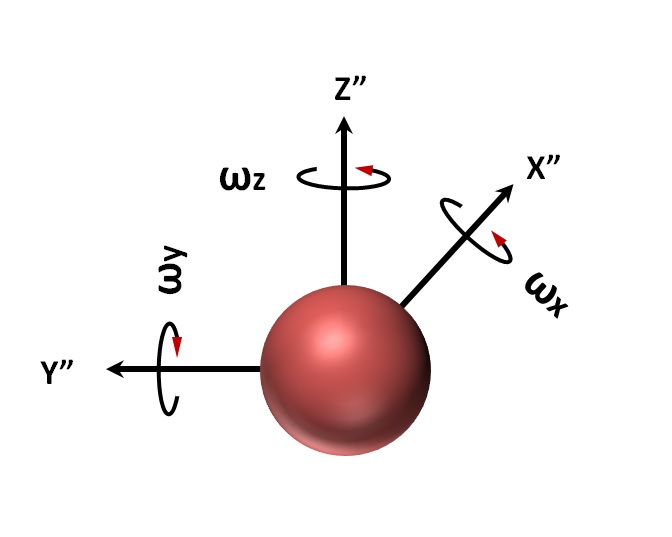
3軸ジャイロセンサ Gyrosensor_ωx_ωy_ωz 状態方程式 ジャイロセンサ から測定した機体座標系の\(X^{\prime \prime}Y^{\prime \prime}Z^{\prime \prime}\)軸回りの角速度成分は、\(ZY’X^{\prime \prime}\)軸回りのオイラー角の時間微分\(\dot{ϕ}, \dot{θ}, \dot{ψ} \)との対応関係は以下の式で表す。
オイラー角で状態方程式の表現 ジャイロセンサの角速度からオイラー角の計算式は以下となる。$$\begin{bmatrix}ϕ\\θ\end{bmatrix} = \begin{bmatrix}ϕ+\dot{ϕ}Δt\\θ+\dot{θ}Δt\end{bmatrix}$$ ただし、\(ψ\)角の積分計算はここで省略する。
誤差の補正 カルマンフィルタおよび本文の及んだ誤差はランダム誤差といい、バイアス誤差はすでにキャリブレーションなどの手法で取り除いたと想定する。加速度センサの精度が悪く、とくに運動中の場合、ただし加速度センサの誤差が蓄積しない。ジャイロセンサの精度が良く、ただしドリフト現象が起きる。ドリフトにより時間とともに誤差がじわじわと蓄積していく。補正手法として、加速度センサにジャイロセンサの出力値を組み合わせて、静的重み係数(経験値)を付ける相補フィルタ の他、時系列分析から異なるセンサの出力値に信頼性に関わる動的重み係数を付ける、いわゆるカルマンフィルタ \((Kalman Filter)\)の再帰的アルゴリズム(手法)がある。フィルタとはランダム誤差(ノイズ)をフィルタリングする意味合いがある。性能からみればカルマンフィルタのほうは優れるのでよく使われる。
\(*\)機体座標系で\(3\)軸加速度センサから傾斜角度と\(3\)軸ジャイロセンサから回転角度を求めて、静的重み付け(経験値)で加算するセンサ融合の手法がある。出典5-をご参照ください。
カルマンフィルタ \(wikipedia:\) カルマンフィルタ\((Kalman Filter,KF\)と略す\()\)は、誤差のある観測値を用いて、ある動的システムの状態を推定あるいは制御するための、無限インパルス応答フィルタの一種である。この解釈では理解できたというわけではなく、以下カルマンフィルタ、拡張カルマンフィルタで状態を推定してみる。
状態空間モデル
一般、汎用的な状態方程式、観測方程式は以下のとおり。
パラメータ初期化
$$\begin{eqnarray*}&& \hat{x}_0 = E[x_0]\\&& \hat{P_0} = E[(x_0-\hat{x_0})(x_0-\hat{x_0})^T]\end{eqnarray*}$$
状態値、共分散行列予測ステップ(t>0)
$$\begin{eqnarray*}&& \bar{x_t} = F_{t-1}(\hat{x}_{t-1})\\&& \bar{P_t} = F_{t-1}\hat{P}_{t-1}F_{t-1}^T + Q_{t-1}\end{eqnarray*}$$ ただし、\(\bar{x_t}\)は予測値、\(\bar{P_t}\)は事前共分散行列、\(Q_{t-1}=E[q_{t-1}q_{t-1}^T]\)
カルマンゲイン、状態値、共分散行列更新ステップ
$$\begin{eqnarray*}&& K_t = \bar{P_t}H_t^T(H_t\bar{P_t}H_t^T + R_t)^{-1}\\
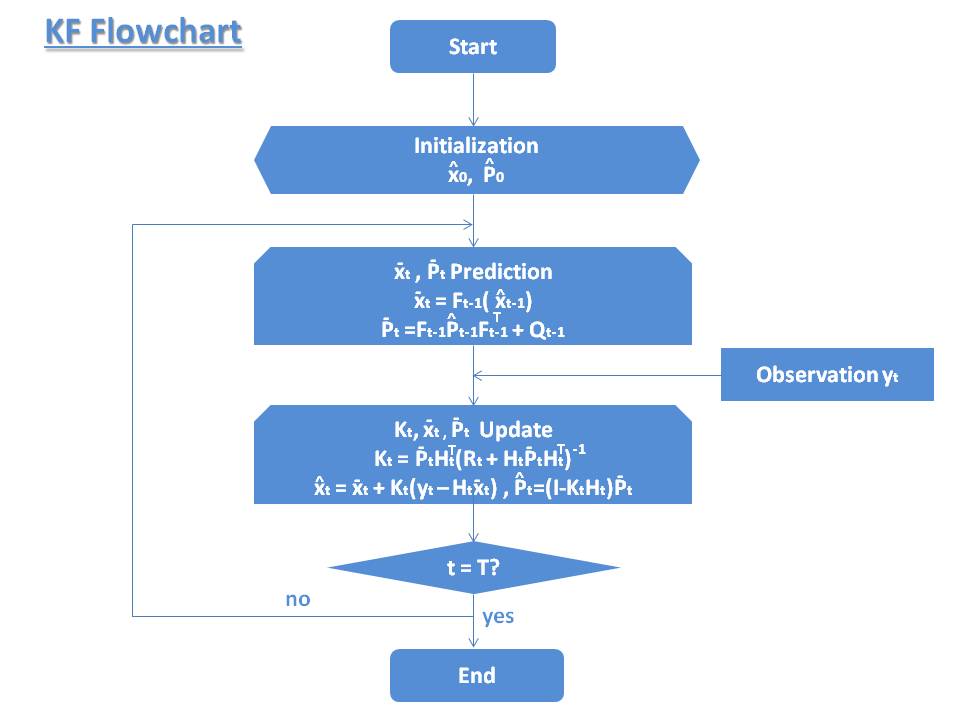
フローチャート
Kalman_Filter_Flowchart_2 導出に関わる参考情報として、本サイト記事 カルマンフィルタの導出 に載ってある。
拡張カルマンフィルタ 拡張カルマンフィルタ \((Extended Kalman Filter,EKF\)と略す\()\)は、非線形フィルタリングである。前述した状態方程式、観測方程式より、以下の状態空間モデルの\(f(⋅)\)または\(H(⋅)\)が非線形関数であり、\(6\)軸\(IMU\)のオイラー角計算に拡張カルマンフィルタは適用される。テイラー展開より、\(2\)次微分以降の項目を省略して、非線形である\(f(⋅)\)の\(1\)次微分を線形化とし、カルマンフィルタのアルゴリズムが適用可能となる。しかし、\(f(⋅)\)の微分では\(f(⋅)\)の一部しか表現できず、この線形化処理(\(1\)次微分)に誤差を大きく招く場合がある。ここでは\(H(⋅)\)は線形関数\(I\)であるため、\(f(⋅)\)のみを線形化する。
状態空間モデル
$$\begin{eqnarray*}&& x_t = f_{t-1}(x_{t-1}^{true}+p_{t-1}) + q_{t-1}\\&& y_t = H_t(x_t^{true}) + r_t\end{eqnarray*}$$
パラメータ初期化
$$\begin{eqnarray*}&& \hat{x}_0 = E[x_0]\\&& \hat{P_0} = E[(x_0-\hat{x_0})(x_0-\hat{x_0})^T]\end{eqnarray*}$$
状態値、共分散行列予測ステップ(t>0)
$$\begin{eqnarray*}&& \bar{x_t} = f_{t-1}(\hat{x}_{t-1})\\&& \bar{P_t} = \hat{F}_{t-1}\hat{P}_{t-1}\hat{F}_{t-1}^T + Q_{t-1}\end{eqnarray*}$$ ただし、\(\bar{x_t}\)は予測値、\(\bar{P_t}\)は事前共分散行列、\(Q_{t-1}=E[q_{t-1}q_{t-1}^T]\)
カルマンゲイン、状態値、共分散行列更新ステップ
$$\begin{eqnarray*}&& K_t = \bar{P_t}H_t^T(H_t\bar{P_t}H_t^T + R_t)^{-1}\\
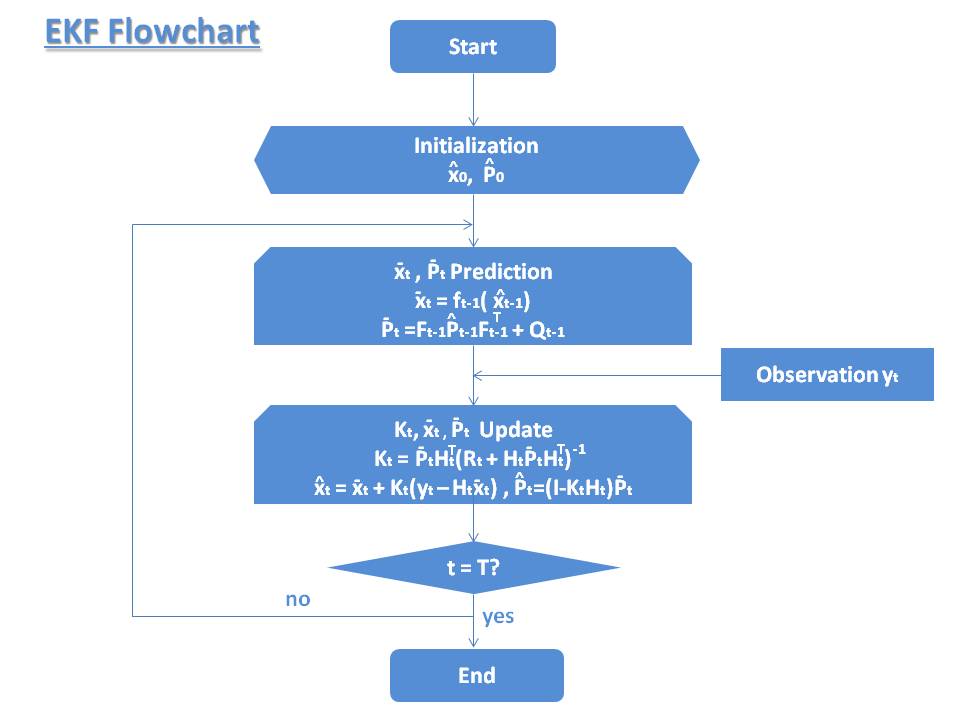
フローチャート
Extended_Kalman_Filter_Flowchart_1 拡張カルマンフィルタを6軸IMUへの適用 状態空間モデルは以下のようになる。
予測値は以下のように求められる。
\(1\)次微分線形化(ヤコビアン行列)は以下のように求められる。
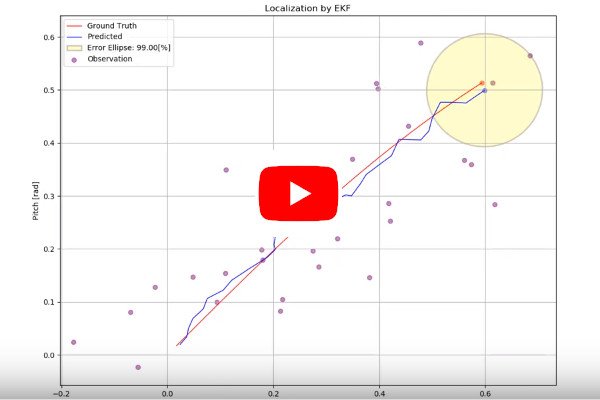
拡張カルマンフィルタによる姿勢推定動作の可視化 拡張カルマンフィルタを実装したPythonスクリプトはGitHubで公開した。imu_ekf Repository@GitHub imu_ekf
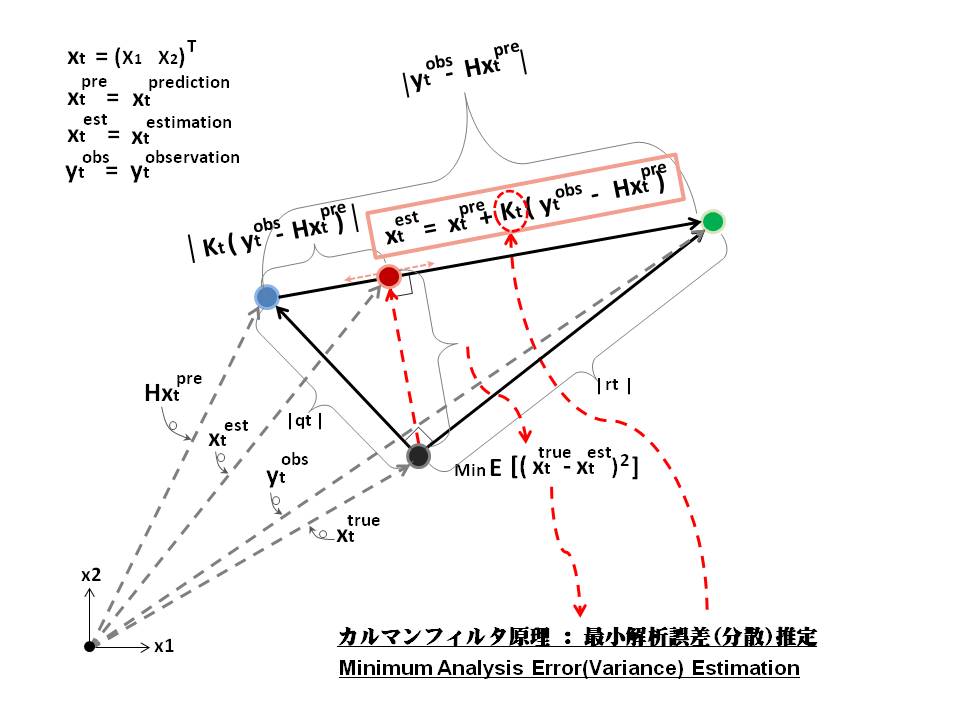
カルマンフィルタの解釈 カルマンフィルタの原理は以下のイメージに示す。kalman_filter_principle_n 状態推定値を予測結果\(x_t\)(実装例ではジャイロセンサーデータ)と観測データ\(y_t\)(実装例では加速度センサデータ)の線形結合で合成し,その誤差(共分散)を最小にする推定法 だと分かる。これはシステム誤差、観測誤差の数学期待が\(0\)のガウス分布との前提条件から由来した推定法である。しかし、カルマンフィルタをかけることで、状態推定値は予測結果と観測データの間にあるのは、真値からかなり乖離してしまう場合にあるのか。これはシステム誤差と観測誤差が無相関かつ直交という前提から、勿論真値が推定値と観測値の間にある結論を結ぶ考えである。また、ジャイロセンサーデータと、加速度センサデータとも観測値\(y_t\)にする方法がある。それぞれのパーフォーマンスの検証は、比較的精確な実験環境(比較用の高精度ジャイロセンサ、加速度センサ、エンコーダ、モータ)はないと、実は容易ではない。というよりも、シミュレーションをかけてカルマンフィルタのアルゴリズムを検証するのが、確実に可能である。
他のフィルタについて \(UKF(Unscented Kalman Filter)\)は、非線形の測量方程式\(F(⋅), H(⋅)\)がテイラー展開より線形化するのではなく、重み付き線形回帰より線形化する手法。\(UKF\)の精度は拡張カルマンフィルタより高いという実験結果はある。また、線形問題に対しては、カルマンフィルタと効果が同様。\(UKF,EKF\)が、状態値、観測値ともガウス分布(正規分布)に従うまたは近似する場合限り、論理的に適用可能とされる。
ロボットSLAM~拡張カルマンフィルタ 上述の拡張カルマンフィルタが\(IMU\)センサへの応用のみならず、同じ理由で、時系列の移動ロボット\(SLAM\)の\(Gmapping\)法にも、エンコーダ情報(オドメトリ情報または\(odom\)情報)とレーザセンサのLidarスキャンマッチング情報をセンサ融合またはセンサフュージョンへ応用される。不整な環境でない限り、\(Lidar\)スキャンマッチング情報のみを使用した\(Hector\)法より精度が良いだろう。不整な環境でエンコーダ情報が正確な位置情報に大いに誤差を招くことがあるから、センサ融合にマイナス効果が出ると考えられる。また、高精度、高スキャンレートの\(Lidar+IMU\)を使用した\(Hector\)法などの手法はある。もう少し詳細な情報は、本サイト記事 SLAM~拡張カルマンフィルタ に載ってある。
参考文献 1-wikipedia: カルマンフィルタ 、オイラー角 Analog Device AN-1057、アプリケーション・ノート、加速度センサーによる傾きの検出 マルチボディダイナミクスの基礎―3次元運動方程式の立て方 基礎からわかる時系列分析 Rで実践するカルマンフィルタ・MCMC・粒子フィルタ センサ融合を加速度センサやジャイロスコープに適用
関連記事 カルマンフィルタの導出 粒子フィルタ SLAM~Unscentedカルマンフィルタ 9軸IMU 6軸/9軸フュージョン 低遅延 USB出力 補正済み ROS対応 YDLIDAR G4=16m 薄型 ROS対応SLAM LIDAR 点検向け自律移動ロボットRED(薄型・小型) 研究開発用 台車型ロボット キット
ロボット・ドローン部品